Symmetry factor of a Wick diagram

[pscplaton]

Hello !

In the book Quantum Field for mathematician, there is this Wick diagram as an example to understand how to compute the symmetry factor (I am sorry, I draw it with paint...)

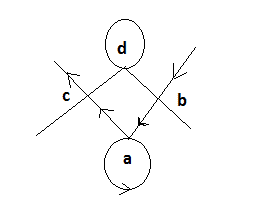
This is about a hermitian field interacting with a complex field. The book says it has a symmetry factor of 2 but I don't understand why, even after reading about symmetry factor on wikipedia (http://en.wikipedia.org/wiki/Feynman_diagram#Symmetry_factors). I don't see what are the two automorphisms of this Feynman diagram... As far as I understand, for a given automorphism, "a" can only be mapped to "a" because of the complex field loop, and the same applies for "d". "c" cannot be mapped to "b" because it has incoming complex propagator from "a", which is not the case of "b"...

Where am I wrong ?

Thanks!

 

[Orodruin]

d is not a complex propagator loop, it has no arrow.

 

[pscplaton]

Yes you are right. I mean that like "a", "d" can only be mapped to itself, because it has a hermitian propagator loop attached, and this is the only hermitian propagator loop of the diagram

 

[Orodruin]

This is the point, you can make the symmetry transformation of changing the direction of this loop without changing the diagram. Hence a symmetry factor of 2.

 

[pscplaton]

Thanks for your reply.

But then I don't understand why the double bubble diagram has a symmetry factor of 2.

According to what you are saying, it should have a symmetry factor of 4, shouldn't it ?

edit: Sorry I was confused. It works. There is actually a symmetry factor of 8