SUMMARY
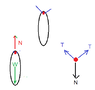
The discussion centers on the concept of normal force in a system involving a ring and a string. Participants clarify that while the ring does contact the string, the normal force is considered internal and thus excluded from the equilibrium equations. The tension in the string can be accurately determined using a free body diagram that accounts for the weight of the ring and the tension forces, while the normal force cancels out in the calculations. This understanding is crucial for solving problems related to equilibrium in physics.
PREREQUISITES
- Understanding of free body diagrams (FBD)
- Knowledge of equilibrium conditions in physics
- Familiarity with tension forces in strings
- Basic concepts of forces including weight and normal force
NEXT STEPS
- Study the principles of static equilibrium in physics
- Learn how to construct and analyze free body diagrams
- Explore the relationship between tension and normal forces in various systems
- Investigate examples of systems with multiple forces acting simultaneously
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, as well as educators seeking to clarify concepts of forces and equilibrium in their teaching materials.