Tainter Damper Figure: Analyzing Forces

[Guillem_dlc]

Homework Statement

1. A "Tainter" damper has the shape of a partial cylinder as shown in the figure. The width of the damper is $12\, \textrm{m}$. Note that the height of the water corresponds to the height of the pivot point of the gate. Calculate the horizontal force in $\textrm{kN}$. Other data: $\rho =1000\, \textrm{kg}/\textrm{m}$, $I_{xx}=bh^3/12$

2. Calculate the vertical force in $\textrm{kN}$

3. Calculate the total force in $\textrm{kN}$

4. Calculate angle of total force in degrees

5. Calculate the momentum of the horizontal force in $\textrm{kNm}$.

Relevant Equations

$F=pA, p=\rho h$

Figure:

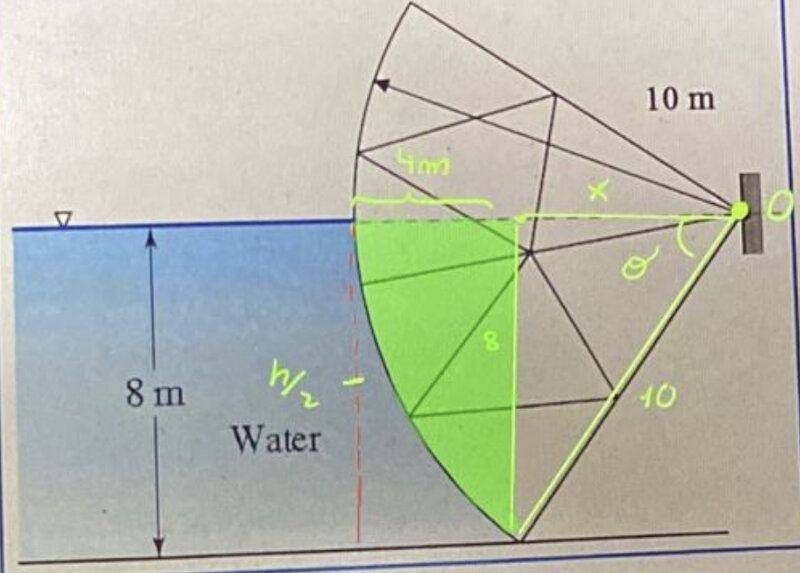
Attempt at a solution:
$$b=12\, \textrm{m},\quad H=8\, \textrm{m}$$
a) $$F_H=p_{CG}A=3767040\, \textrm{N}=\boxed{3767,04\, \textrm{kN}}$$
$$A=8\cdot 12=96\, \textrm{m}^2$$
$$p_{CG}=\rho_g h_{cg}=39240\, \textrm{Pa}$$
b) $$F_V=mg=\rho_g V$$
We calculate $\theta \rightarrow 8=10\cdot \sin \theta \rightarrow \dfrac{8}{10}=\sin \theta \rightarrow \theta =53,13\, \textrm{º}$
$$x=10\cdot \cos (\theta)=6\, \textrm{m}$$
We calculate $A\rightarrow A=\dfrac{\pi r^2\cdot 53,13}{360}=\dfrac{6\cdot 8}{2}=22,3647\, \textrm{m}^2$
$$F_V=\rho_gV=\rho_g bA=\boxed{2632,77\, \textrm{KN}}$$
c) First of all we find $\alpha$ (angle between forces).
$$\alpha =\arctan \dfrac{F_V}{F_H}=34,95\, \textrm{º}$$
$$F=\dfrac{F_H}{\cos \alpha}=\boxed{4595,88\, \textrm{kN}}$$
d) $$\boxed{\alpha =34,95\, \textrm{º}}$$
e) First and foremost, we must locate the centre of pressure (CP).
$$y_{CP}=-\dfrac{\rho_g I_{xx}}{F_H}=-1,333\, \textrm{m}$$
$$M_o=F_H\cdot h_{cp}=F_H\cdot (4+1,333)=\boxed{20089,62\, \textrm{kN}\cdot \textrm{m}}$$
Does this one look good to you?

 

[haruspex]

Think again about the volume displaced in part b.

 

[Guillem_dlc]

Think again about the volume displaced in part b.

Wouldn't this be it, or would it affect everything? I can see well how I've done it, can't I?

 

[Guillem_dlc]

Okay, maybe like this?

 

[erobz]

Figure:
View attachment 316081

e) First and foremost, we must locate the centre of pressure (CP).
$$y_{CP}=-\dfrac{\rho_g I_{xx}}{F_H}=-1,333\, \textrm{m}$$

Again... That is not the formula for $y_{CP}$. What you are using is the formula for $\bar y - y_{CP}$. They are not the same thing. It's obvious you understand that is not $y_{cp}$ from the remainder of your calculation, which is why it's confusing that you keep calling it that.

As for everything else, it seems to check out.

 

[haruspex]

Okay, maybe like this?
View attachment 316091

No.
It's a bit tricky. Suppose, instead of the sector of a circle given, the damper were to continue further to the right. Would that change the force? Would it change your calculation?
The area you have shaded would be correct if there were also water to the right. In that scenario, can you see a way to split the damper into two parts such that the water on the left is responsible for the buoyancy force on the left part and the water on the right responsible for that on the right part?

 

[Guillem_dlc]

No.
It's a bit tricky. Suppose, instead of the sector of a circle given, the damper were to continue further to the right. Would that change the force? Would it change your calculation?
The area you have shaded would be correct if there were also water to the right. In that scenario, can you see a way to split the damper into two parts such that the water on the left is responsible for the buoyancy force on the left part and the water on the right responsible for that on the right part?

And what I have marked in the figure at the beginning of everything, neither?

 

[haruspex]

And what I have marked in the figure at the beginning of everything, neither?

What is highlighted in post #1 is correct, but I looked at your working and you do not seem to have subtracted the triangular portion. I see $A=\pi r^2\frac{\theta}{2\pi}$.

 

[erobz]

What is highlighted in post #1 is correct, but I looked at your working and you do not seem to have subtracted the triangular portion. I see $A=\pi r^2\frac{\theta}{2\pi}$.

They did. it's a typo.

We calculate $A\rightarrow A=\dfrac{\pi r^2\cdot 53,13}{360}=\dfrac{6\cdot 8}{2}=22,3647\, \textrm{m}^2$

Should read:

We calculate $A\rightarrow A=\dfrac{\pi r^2\cdot 53,13}{360}-\dfrac{6\cdot 8}{2}=22,3647\, \textrm{m}^2$

 

[haruspex]

They did. it's a typo.


Should read:

Aha!

 

[erobz]

The only potential issue I can see with this method of converting the problem (which, isn't an issue for the questions you had to answer), what would you do if you actually had to locate the center of pressure $CP (x_{cp},y_{cp} )$? I have a feeling you would find it in a place where it doesn't seem like it should be w.r.t the actual scenario. The question: Is it just a simple transformation back to the actual scenario?