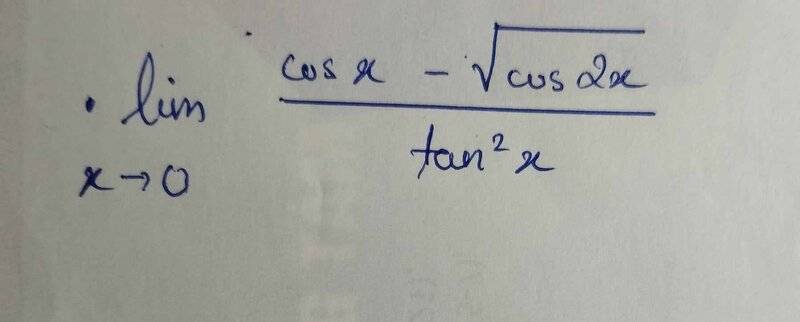Homework Help Overview
The discussion revolves around evaluating the limit of a fraction involving trigonometric functions, specifically the expression f(x) = (cos x - √(cos 2x)) / (tan^2 x) as x approaches 0. Participants explore various approaches to simplify the expression using trigonometric identities and limits.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants suggest expressing the function in terms of cos x and exploring the limit as a function of cos x. There are discussions about misunderstanding the application of limits and the potential use of L'Hôpital's rule. Some participants propose factoring or multiplying by the conjugate to simplify the expression.
Discussion Status
The discussion is active with multiple participants providing different perspectives on how to approach the limit. Some guidance has been offered regarding the use of trigonometric identities and the structure of the limit, but there is no explicit consensus on a single method or solution yet.
Contextual Notes
Participants express uncertainty about the instructions given by a teacher and question the clarity of the problem setup. There are indications of differing interpretations of how to manipulate the limit expression effectively.