- #1
dozzer
- 3
- 0
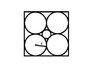
In this diagram, a square is inscribed with four circles of equivalent size, all with the radius of 1. Each circle is tangent to two sides of the square, two circles, and the smaller circle. Obviously each side of the square is equal to 4, but what is the radius of the smaller circle?
I think the answer is something like 21/2 -1, or .414..., but how would you solve for it?
This is a problem from the SAT before the math section was reformed.
I think the answer is something like 21/2 -1, or .414..., but how would you solve for it?
This is a problem from the SAT before the math section was reformed.