Taylor series in terms of discrete derivative

[Jhenrique]

All analitic function can be express how: $$f(x) = \frac{1}{0!} \frac{d^0f}{dx^0}(x_0) (x - x_0)^0 + \frac{1}{1!} \frac{d^1 f}{dx^1}(x_0) (x - x_0)^1 + \frac{1}{2!} \frac{d^2f}{dx^2}(x_0) (x - x_0)^2 + \frac{1}{3!} \frac{d^3f}{dx^3}(x_0) (x - x_0)^3 + ...$$ that is the taylor series of the function f(x).

Analogously, should exist a taylor series that use the discrete derivative $\frac{\Delta f}{\Delta x} = f[x+1] - f[x]$. I found this

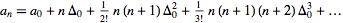in wolframpage http://mathworld.wolfram.com/ForwardDifference.html but appears strange. I didn't undertood what such series means. Someone can explain me?

 

[pwsnafu]

I'm going to use notation from time scale calculus, which is a unification of continuous and discrete calculus. It makes my message more obvious.

A time scale is a non-empty closed subset $\mathbb{T}\subset\mathbb{R}$.
Given a function $f : \mathbb{T}\to\mathbb{R}$, we define the (Hilger) derivative $f^{\Delta}$ in such a way such that

• if $\mathbb{T} = \mathbb{R}$ then Hilger derivative is equal to $f^{\Delta}(t) = f'(t)$ and
• if $\mathbb{T} = \mathbb{Z}$ then Hilger derivative is equal to $f^{\Delta}(t) = \Delta f(t)$.

To study the Taylor theorem, we also have "h-polynomials" which are defined
$h_{0}(t,s) = 1$ and
$h_{k+1}(t,s) = \int_s^t h_k(\tau, s) \, \Delta \tau$.
In words "start with the constant and keep integrating over and over".

• if $\mathbb{T} = \mathbb{R}$ then $h_k(t,s) = \frac{(t-s)^k}{k!}$ and
• if $\mathbb{T} = \mathbb{Z}$ then $h_k(t,s) = \frac{(t-s)(t-s-1)(t-s-2)\ldots(t-s-k+1)}{k!}$

The Taylor theorem itself is
$f(t) = \sum_{k=0}^{n-1}f^{\Delta^k}(a)\, h_{k}(t, a) \, + R$
where R is the remainder (I'm not going to write down the remainder term).

• if $\mathbb{T} = \mathbb{R}$ then
  $f(t) = f(a) + f'(a) \frac{t-s}{1!} + f''(a) \frac{(t-s)^2}{2!}+\ldots+f^{(k)}(a) \frac{(t-s)^k}{k!} + \ldots$ and
• if $\mathbb{T} = \mathbb{Z}$ then
  $f(t) = f(a) + \Delta f(a) \frac{t-s}{1!} + \Delta^2 f(a) \frac{(t-s)(t-s-1)}{2!}+\ldots+\Delta^{k}f(a) \frac{(t-s)(t-s-1)\ldots(t-s-k+1)}{k!} + \ldots$.

The important thing is that in discrete calculus these $\frac{(t-s)(t-s-1)(t-s-2)\ldots(t-s-k+1)}{k!}$ serve the same role as $\frac{(t-s)^k}{k!}$ does in the continuous calculus.

 

[Jhenrique]

good answer!