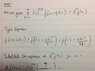jammyloller
- 1
- 0
Question:
http://i.imgur.com/GsjeL.png
Here is my attempt so far:
http://i.imgur.com/AyOCm.png
Note: I've used m where the question has used j.
My attempt is based off some bad notes I took in class so the way I am trying to solve the problem may not be the best. I'm struggling to work out how to continue from the part where I've left a question mark, and I'm not even sure if the Taylor expansion is correct.
Could anybody offer some thoughts as to what to do?
http://i.imgur.com/GsjeL.png
Here is my attempt so far:
http://i.imgur.com/AyOCm.png
Note: I've used m where the question has used j.
My attempt is based off some bad notes I took in class so the way I am trying to solve the problem may not be the best. I'm struggling to work out how to continue from the part where I've left a question mark, and I'm not even sure if the Taylor expansion is correct.
Could anybody offer some thoughts as to what to do?