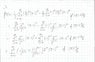Taylor series using Geometric Series

[jegues]

Let $$f(x) = \frac{4-4x}{4x^{2} -8x -5};$$ given the partial decomposition,


$$\frac{4-4x}{4x^{2} -8x -5} = \frac{1}{5-2x} - \frac{1}{1+2x},$$



find the Taylor series of f(x) about 1. Express your answer in sigma notation and simplify as much as possible. Dtermine the open interval of convergence.

See figure attached for my attempt.



Did I a mistake converting each piece into a taylor series by use of geometric series?



Also I can't think of how to simplify this anymore, but this may be due to a mistake in the first portion of my work.



Does anyone see any problems in my work?



Thanks again!

 

[Mark44]

You have |x - 1| < 3/2, from which you conclude |x| < 5/2, which is incorrect.
|x - 1| < 3/2
==> -3/2 < x - 1 < 3/2
==> -1/2 < x < 5/2

Also, that -2/3 that you're asking about. It seems to me that it shows up in (-2/3)ⁿ.

 

[jegues]

You have |x - 1| < 3/2, from which you conclude |x| < 5/2, which is incorrect.
|x - 1| < 3/2
==> -3/2 < x - 1 < 3/2
==> -1/2 < x < 5/2

Also, that -2/3 that you're asking about. It seems to me that it shows up in (-2/3)ⁿ.

So for the radius of convergence I can't take the 1 out? I must keep it as,

|x - 1| < 3/2 ?

But then, when I want the open interval of convergence then I can take the 1 out like so,

-1/2 < x < 5/2

Is that what you are trying to say?

Aside from that is there any errors in the way in which I produced the Taylor series for f(x)? And should I be able to simplify more than what I have?

 

[Mark44]

The radius of convergence is 3/2 (for that one series). The interval of convergence is -1/2 < x < 5/2. The series might converge at the endpoints - you have to check them separately.

I didn't notice anything else, but then your scan looks like it's in pencil, so is a little hard to read.

 

[jegues]

The radius of convergence is 3/2 (for that one series). The interval of convergence is -1/2 < x < 5/2. The series might converge at the endpoints - you have to check them separately.

I didn't notice anything else, but then your scan looks like it's in pencil, so is a little hard to read.

So is the final expression I have as simplified as it can get? I can't think of what else to do and the question says simplify as much as possible.

 

[Mark44]

I would combine the two series into one summation.

 

[jegues]

I would combine the two series into one summation.

I did that on the last line of my work didn't I?

 

[Mark44]

I was having a hard time trying to follow your work in two different places. In the 2nd thumbnail, between line 2 and line 3, there's a sign that mysteriously changes from - to +. Also, you have |x| < 5/2, which isn't correct.

 

[jegues]

I was having a hard time trying to follow your work in two different places. In the 2nd thumbnail, between line 2 and line 3, there's a sign that mysteriously changes from - to +. Also, you have |x| < 5/2, which isn't correct.

From line 2 to 3 I took the negative 1 outside the sum and put it inside the sum. So,

$$(-1)^{n} \rightarrow (-1)^{n+1}$$

I understand that |x| < 5/2 is from our previous discussion.

Aside from that mistake, is there anything else I should be doing in this problem to simplify more?

Most of the times we've done these problems in class and in homework they've simplified nicer than this.

The answer I have (aside from the error you mentioned) could be perfectly fine, I'm just not sure.

 

[Mark44]

I don't see anything else. It looks OK to me.

 

[jegues]

I don't see anything else. It looks OK to me.

I found another error right at the beginning.

$$7 - 2(x-1) \neq 5-2x$$

I'm going to change this and reattempt the problem from the beginning.

I'll post my results.

 

[vela]

Hmm, the function is odd about x=1, so you should end up with only odd powers of (x-1). You can see it's odd if you rewrite the original function as

$$\frac{4-4x}{4x^2-8x-5} = -\frac{4(x-1)}{4(x-1)^2-9}$$

Based on the expansions I got out of Mathematica, I'll suggest your series with the 7s in it is wrong. You should recheck your algebra.

EDIT: Oh, I see you already probably found the mistake.

 

[jegues]

Here's my 2nd attempt. (See Figure Attached)

Things look a lot better this time, I just want to be sure I am simplifying it as much as it can possibly be simplified.

How's it look?

 

[vela]

You can simplify it a bit more. (Try writing out the first few terms.) Also, did you check for convergence of the endpoints?

 

[jegues]

You can simplify it a bit more. (Try writing out the first few terms.) Also, did you check for convergence of the endpoints?

I don't need to check for convergence of the endpoints because the questions asks for the open interval of convergence.

As far as simplifying after opening the series I think it can be rewritten as,

$$\sum_{n=0}^{\infty}\frac{2^{n+1}}{3^{n+1}}(x-1)^{n} \text{ if } |x-1| < \frac{3}{2}$$

Could I have realized this from what I had without rewriting the series in open form by using algebra? If so, how?

Let me know what you think.

Thanks again.

 

[vela]

That's not quite right. It's close though. You found the series has only odd powers, right? Your expression has both even and odd terms.

 

[jegues]

That's not quite right. It's close though. You found the series has only odd powers, right? Your expression has both even and odd terms.

Whoops I think I see it now. Let me try this again,

$$\sum_{n=0}^{\infty} \frac{2^{2(n+1)}}{3^{2(n+1)}}(x-1)^{2n+1} \text{ if } |x-1| < \frac{3}{2}$$

Hopefully this one works.

 

[vela]

Yeah, that looks right. You could make the numerical factor a tad simpler by writing it as (4/9)ⁿ⁺¹, but that's just nit-picking.