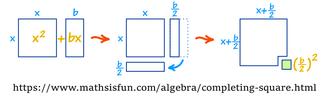
I apologize for summarizing the discussion for my own clarification.
As you all know, solving a quadratic equation is showing how to find two numbers, r,s if one knows their sum r+s and their product rs. I.e. the solutions, r,s, of x^2 - bx + c = 0, satisfy r+s = b, and rs = c. The key idea is that if one could also find their difference, one would be done. i.e. (r+s) + (r-s) = 2r, and (r+s)-(r-s( = 2s.
All solutions are then based on these two formulas, which show that the square of the sum, and the square of the difference, are equivalent up to a multiple of the product:
(r+s)^2 = r^2 + 2rs + s^2;
(r-s)^2 = r^2 -2rs + s^2.
Consequently, (r-s)^2 = (r+s)^2 - 4rs.
Thus, if one knows the sum of two numbers, and their product, hence the right hand side of this equation, one can find the square of their difference, i.e. the left hand side. Then by taking a square root one finds also their difference.
I.e.square the sum, and subtract 4 times the product, and one has the square of the difference,
Since knowing both the sum and the difference of two numbers gives both numbers, it follows that one can find two numbers if we know their sum and product.
Thus to solve x^2 - bx + c = 0, for roots r,s, we know r+s = b and rs = c. Hence (r-s)^2 = b^2-4c.
Hence (r-s) = sqrt(b^2-4c), so 2r = (r+s) + (r-s) = b + sqrt(b^2-4c).
Similarly, 2s = b - sqrt(b^2-4c).
Thus r,s = (1/2)(b±sqrt(b^2-4c)).
This is the way I personally like to understand the solution of quadratic equations, essentially the method of Diophantus.
The reason I like this is I can understand the reason for every step. In high school when I read the derivation of the final formula, by completing the square, it seemed to me entirely unmotivated, and looked clunky and ugly. Over 50 years later, when I finally encountered Lagrange's clear explanation, I at last felt satisfied about it.
I had memorized the formula in high shool, and always had success using it, but never felt that I understood how someone would have thought of it. That is always my goal. So this is to me another argument for reading the classics, i.e. the masters.