I Teeter-Totter Rotation Direction with Different Connections

[johnrot]

(I don't know what happened with my topic so I will post it again...)

this is my half weird teeter with pivot point at (B)
and we have two solution for conection ,rigid conection and with universal joint..
this is example how type of conection can change direction of rotation..

basics question is :in what direction will teeter rotate about pivot point (B)..

rigid conection

universal joint conection

Do you agree with my conclusion and moment equation?

 

[fresh_42]

(I don't know what happened with my topic so I will post it again...)

The machinery often sets posts from new members which have an attachment into the state: to be moderated. So as long nobody took a look at it and approved it, it remains in that state. This happens, too, if you edit the post. Then again, the automatism checks the attachments and sets it on hold. It is a bit annoying, I know, but it also fishes dozens of spam posts.

 

[A.T.]

(I don't know what happened with my topic so I will post it again...)

this is my half weird teeter with pivot point at (B)
and we have two solution for conection ,rigid conection and with universal joint..
this is example how type of conection can change direction of rotation..

basics question is :in what direction will teeter rotate about pivot point (B)..

rigid conection
https://www.physicsforums.com/attachments/261100
universal joint conection
View attachment 261101Do you agree with my conclusion and moment equation?

Why is the rope not in tension in the first case?

As for your argument: Make sure you have the directions and magnitudes of the forces on the teeter by feet and UJ right. Draw a diagram where they are shown.

 

[johnrot]

Why is the rope not in tension in the first case?

As for your argument: Make sure you have the directions and magnitudes of the forces on the teeter by feet and UJ right. Draw a diagram where they are shown.

I forgot to write,but rope is in tension,I add it now...

rope is 100% horizontal so at men feet is all men weight(W),horizontal forces " rope tension" at feet and U.J. cancel each other out,so we have Thrust and W..so rotation is in counter clockwise direction,but ground will stop this rotation...

Do you agree with me that teeter with U.J. case have tendency to rotate about point B in counter clockwise direction,opposite from case with rigid conection?that is idea of this experiment,so we change direction of rotation with different type of conection?So if we put weight scale below teeter ,when we increase fan Thrust ,weight scale will increase weight numbers..

 

[A.T.]

rope is 100% horizontal so at men feet is all men weight(W),horizontal forces " rope tension" at feet and U.J. cancel each other out,so we have Thrust and W..so rotation is in counter clockwise direction,but ground will stop this rotation...

You have drawn two forces at UJ. Which one is acting on the teeter?

Assume the propeller mast is massless, so forces and moments on it have to balance. Does your solution satisfy this condition, for arbitary rope height to mast height ratios?

 

[johnrot]

You have drawn two forces at UJ. Which one is acting on the teeter?

Assume the propeller mast is massless, so forces and moments on it have to balance. Does your solution satisfy this condition, for arbitary rope height to mast height ratios?

Dont understnad your question..
Yes this is internal forces at U.J. one is from rope tension ,one is from fan thrust..
Yes men is in balance with propeler mast..

Do you agree with me that teeter with U.J. case have tendency to rotate about point B in counter clockwise direction,opposite from case with rigid conection?that is idea of this experiment,so we change direction of rotation with different type of conection?So if we put weight scale below teeter ,when we increase fan Thrust ,weight scale will increase weight numbers..

 

[A.T.]

Dont understnad your question..

What is the direction of the force by the mast on the teeter?

 

[jbriggs444]

You are trying to draw conclusions about how the scale reading will change when you turn the fan on or off.

But turning the fan on or off is not the only change you have to make. When you turn it on, the fellow on the teeter has to lean back. When you turn it off, the fellow on the teeter has to return to a vertical posture.

 

[johnrot]

]

What is the direction of the force by the mast on the teeter?

to the left,
sum of horizontal forces at feet and u.j. is equal to thrust with direction to the right..

 

[johnrot]

You are trying to draw conclusions about how the scale reading will change when you turn the fan on or off.

But turning the fan on or off is not the only change you have to make. When you turn it on, the fellow on the teeter has to lean back. When you turn it off, the fellow on the teeter has to return to a vertical posture.

I just want to prove that in case of U.J. conection you can not rotate teeter in clockwise direction about teeter pivot point B, whatever you do with fan thrust or with your body position.
Isnt it obvious with just one look at the picture?

 

[jbriggs444]

I just want to prove that in case of U.J. conection you can not rotate teeter in clockwise direction about teeter pivot point B, whatever you do with fan thrust or with your body position.
Isnt it obvious with just one look at the picture?

If you hold the person in place, rotating him around his center of mass then, as you increase fan thrust, you will be moving his feet farther and farther right, reducing the counterclockwise torque on the teeter from that source.

Viewed as a logical puzzle, there is nothing that prevents the feet from moving out past the teeter's pivot point resulting in a net clockwise torque.

Viewed as a physical puzzle, the feet will run out of teeter first.

 

[johnrot]

If you hold the person in place, rotating him around his center of mass then, as you increase fan thrust, you will be moving his feet farther and farther right, reducing the counterclockwise torque on the teeter from that source.

Viewed as a logical puzzle, there is nothing that prevents the feet from moving out past the teeter's pivot point resulting in a net clockwise torque.

Viewed as a physical puzzle, the feet will run out of teeter first.

I write that test is stopped if men is pulled by thrust,I only look for situations where men and mast-thrust is in balance...
So I basicly want to prove with my experiment that universal joint can not transfer moment,because some my friends don't understand that,so I don't know what is best way to explain them...only that..
i

 

[jbriggs444]

If the man is moving his feet and you are not concerned with that then it is not a fair test. You are cheating the people you are arguing with.

Yes, I agree with the point that as long as the feet are confined to the teeter, the teeter cannot be tipped clockwise by the fan in the case of a mast that is free to pivot.

 

[johnrot]

Yes, I agree with the point that as long as the feet are confined to the teeter, the teeter cannot be tipped clockwise by the fan in the case of a mast that is free to pivot.

We are debate only for that option,so feet stay at teeter and don't move/slide...

How you will best explain to someone that u.j. can't transfer moment,only forces?

 

[johnrot]

now I see that I choose wrong example because even with mebers -experts of physics I have hard time to explain what is my point..maybe my example is to messy
I thought that we will solve this at first post...

 

[A.T.]

so we change direction of rotation with different type of conection?

Are you saying that all the external forces on the whole thing stay the same, but the net moment on it changes direction, because you changed some internal connection?

 

[jrmichler]

asics question is :in what direction will teeter rotate about pivot point (B)..

The moment equation in your top diagram of the OP is correct. If the fan thrust times its height above pivot B is greater than weight W times its horizontal distance from the pivot B, the whole assembly will rotate clockwise until the fan smashes into the ground.

If the weight W times its horizontal distance from the pivot B is greater than the fan thrust times its height above the pivot B, the assembly will rest on the support under the person.

The rope in tension, the skidding force on the man's feet, the bending of the column supporting the fan are all internal forces and are ignored for the purpose of studying whether the entire assembly will move. Internal forces are internal forces, and are relevant only if you want to know if the man's feet will slip, if the rope will break, or if the fan column will flop over.

But all of this is academic when you support the fan column with a universal joint because the fan column will flop sideways (in or out of the screen) and the fan will crash into the ground.

 

[johnrot]

Are you saying that all the external forces on the whole thing stay the same, but the net moment on it changes direction, because you changed some internal connection?

no
I just want to say next:
1) for rigid conection ; if , Thrust x H > W x D ,teeter will rotate clockwise,(so with fan thrust you can rotate teeter clocwise)

2)for U.J. conection: when you turn ON fan, teeter will try rotate conuter clockwise,it will push at the ground,so if you put weight scale below teeter ,weight scale will increase reading,
but assumptions are that feet do not slip and men and mast of fan is in balance,(so when fan is turn ON and men and mast is in balance,teeter has counter clockwise torque)

so with different conection we change teeter direction of rotation,yes it sounds very weird,but that's the way it is

(but normaly if you increase fan thrust too much ,that will slide or bring down men to the right,mast will come in contact with teeter construction and teeter will agian rotate clockwise,but then men and mast is not in balance,so my assumption is violated)

 

[johnrot]

Internal forces are internal forces, and are relevant only if you want to know if the man's feet will slip, if the rope will break, or if the fan column will flop over.

Every external force can be replaced by internal forces..
So external forces Thrust and W at man c.g. can be repalce for internal forces at feet and U.J.(horizontal and vertical components)...and you must get same result when calculating tasks..

 

[A.T.]

Are you saying that all the external forces on the whole thing stay the same, but the net moment on it changes direction, because you changed some internal connection?

no

So what is the change in external forces that causes the net external moment on the whole thing to change direction?

 

[johnrot]

So what is the change in external forces that causes the net external moment on the whole thing to change direction?

isnt my task so obvious with any calculation?

rigid conection
calculation for minimum thrust force for teeter rotation :
thrust x 1.5m > 100kg x 1.93m... thrust=128kg ...so if thrust is equal or bigger than 128kg than teeter will rotate in clockwise direction...than weight scale= 0kg

u.j.conection

calculate tension in rope:
100kgxcos20=Txsin20
T=274kg

calculate Thrust force
274kgxsin20=Thrustx2m
Thrust=46kg
(men can not achive 128kg of thrust force,becuse it will be slide or bring down"catapult" to the right,maximum theoretical thrust that men can achieve with U.J. case is 50kg)

calcualte weight on scale
weight scale=Thrustx0.5m + Wx1m=46kgx0.5 + 100x1m
weight scale=123kg
differnet teeter desing

 

[A.T.]

(men can not achive 128kg of thrust force,becuse it will be slide or bring down"catapult" to the right,maximum theoretical thrust that men can achieve with U.J. case is 50kg)

So the whole point is that with limited floor space you cannot create arbitarily large rope tension, by leaning into the rope?

 

[jbriggs444]

isnt my task so obvious with any calculation?

Not really. I was forced to reverse engineer your reasoning process by looking at the numbers in your equations.

As I understand it, your point was to deduce that

1. 128 kg thrust is required to balance the teeter.
2. The man cannot counterbalance 128 kg thrust even if he leans back at 20 degrees from the horizontal
3. For a fixed thrust, the higher the teeter is raised over the pivot point, the less clockwise torque is required to support it against tipping left.

I agree with all three points.

Let me try to show your work...

You begin with a calculation for the "rigid connection" case. No drawing is supplied. However, the first drawing with the universal joint replaced with a fixed joint would be apt.

You appear to have a 2 meter mast, a man that is perched 1.93 meters to the left of the pivot point and a teeter that is depressed 0.5 meters below the pivot point. The 1.93 meter displacement is because the man is leaning back at an steep angle, making 20 degrees from the horizontal. The man's feet are 1 meter left from the pivot and his center of gravity is 1 meter away on the diagonal. The cosine of 20 degrees is 0.93.

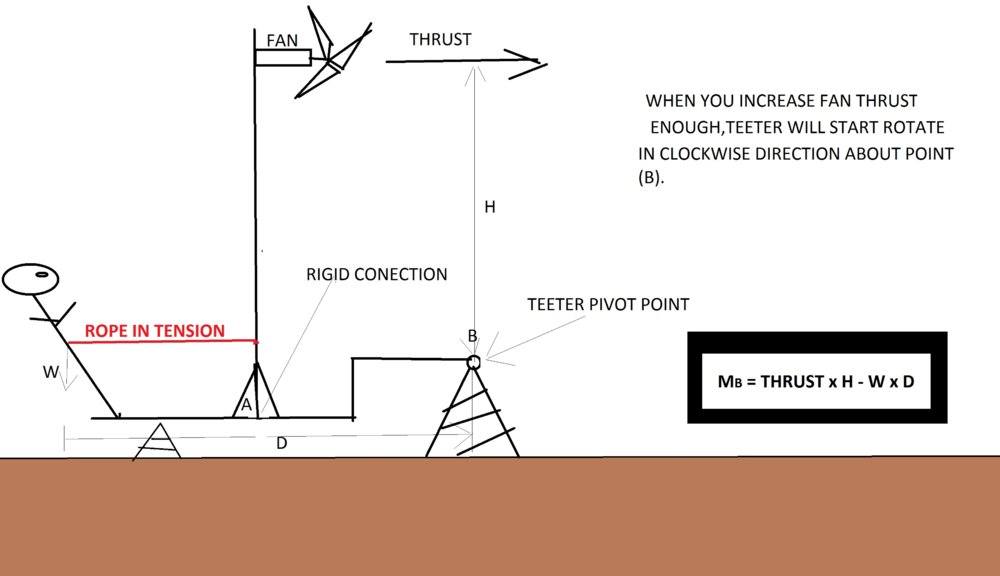
You equate the torque from the man (100 kg * 1.93 meters counterclockwise) with the torque from the fan (thrust * 1.5 meters clockwise) to deduce that the two balance when thrust is 128 kg.

If you'd done the calculation more accurately, you'd have gotten 129 kg.

rigid conection
calculation for minimum thrust force for teeter rotation :
thrust x 1.5m > 100kg x 1.93m... thrust=128kg ...so if thrust is equal or bigger than 128kg than teeter will rotate in clockwise direction...than weight scale= 0kg

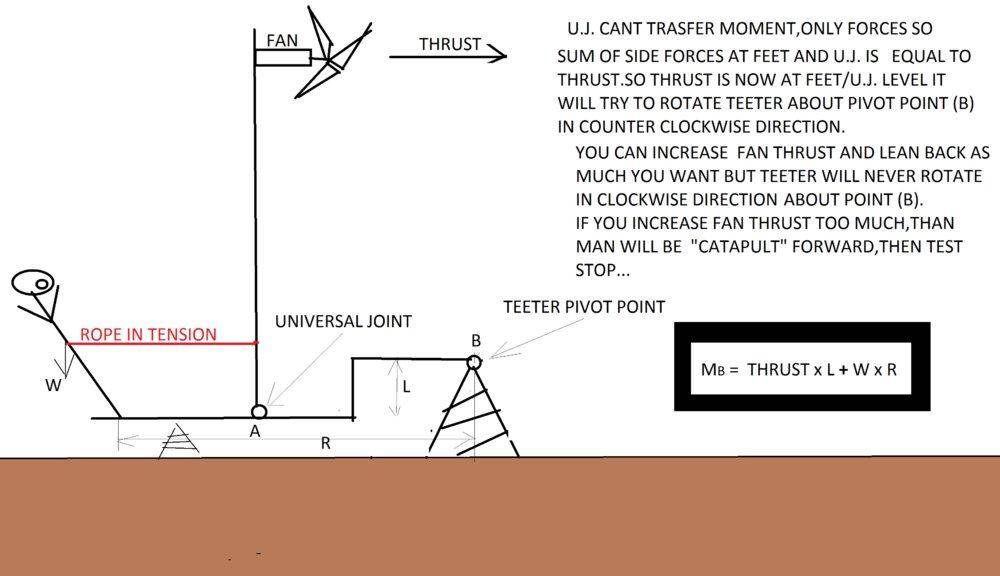
Now you draw the same scenario, this time with a universal joint

u.j.conection
View attachment 261161

Again the 100 kg man is leaning back at a steep angle so that he makes 20 degrees from the horizontal. Because the mast is free to swivel, this constrains the thrust that the fan must make. You proceed to calculate that.

You equate torques about the man's feet. His weight times the horizontal displacement of his center of gravity from his feet is equal to the rope tension times the vertical attachment point of the rope.

You've skipped the step where the man's height cancels out of the equation by making an unstated assumption: The rope is attached at the man's center of gravity.

100kgxcos20=Txsin20
T=274kg

Let us check the numbers. Tension = 100 kg times the cotangent of 20 degrees = 274 kg. Check.

Now you proceed to calculate the thrust of the fan.

Now you work with torques about the universal joint. It seems that the 1m on the drawing is the height of the man's center of gravity when standing vertically. Since he is leaning back at a very sharp angle, the vertical height of that center of gravity is much reduced. The rope is apparently supposed to be horizontal. [Perhaps it is greased and is free to slide up and down the mast].

You equate the counter-clockwise torque from the rope tension with the clockwise torque from the fan:

calculate Thrust force
274kgxsin20=Thrustx2m
Thrust=46kg

Checking those figures, it seems that you have rounded 46.8 down to 46. A better figure would be 47 kg.

You proceed to make a comment that seems to relate to the force of static friction. That the man cannot lean back any farther without his feet sliding out from under. So he is limited to balancing a thrust of about 50 kg (apparently rounding your computed 46 kg up to 50 kg).

(men can not achive 128kg of thrust force,becuse it will be slide or bring down"catapult" to the right,maximum theoretical thrust that men can achieve with U.J. case is 50kg)

Yes, I agree with all of this so far.

You proceed to calculate the displayed weight on the scale. This time you are equating torques about the pivot point of the teeter.

The net horizontal component of the external force of man and mast on the teeter has to match the external force from the fan. Both components of that force (from the man's feet and from the universal joint at the bottom of the mast) are 0.5 meters below the pivot point. So that's a counter-clockwise torque of thrust * 0.5 m.

The net vertical force on the teeter has to match the weight of the man. The man's weight is 100 kg force and this force is applied to the teeter at the man's feet. [The mast can exert no vertical force since it is massless, since the rope is horizontal and since the fan thrust is horizontal]

calcualte weight on scale
weight scale=Thrustx0.5m + Wx1m=46kgx0.5 + 100x1m
weight scale=123kg

Yes, I agree.

You then proceed to shift whole assembly to 0.5 m above the pivot point, giving the 46 kg fan thrust an extra 1 meter of moment arm and note that the weight scale reading is reduced by 46 kg.

differnet teeter desing
View attachment 261162

Yes, I agree.

 

[johnrot]

Not really. I was forced to reverse engineer your reasoning process by looking at the numbers in your equations.
The net horizontal component of the external force of man and mast on the teeter has to match the external force from the fan. Both components of that force (from the man's feet and from the universal joint at the bottom of the mast) are 0.5 meters below the pivot point. So that's a counter-clockwise torque of thrust * 0.5 m.

You are very very good at explaining my calculation.Thumbs up!
Yes ,rope is attached at c.g.

But I still think that we didnt have to do calculations to solve problem..

Here is why:
We must just know basic universal joint rule,that U.J. CAN NOT TRANSFER MOMENT ,ONLY FORCES.
So with that rule applaying on our case we can see that "thrust" force "act" in level of U.J., so now "thrust" is 0.5m below pivot point B ,so it make counter clockwise rotation..

(50kg max thrust is not rounding 46 number, I just want to say that this is maximum theoretical thrust when men lean angle is zero degrees(horizontal) so 100kg x 1m =Thrust x 2m...Thrust =50kg but this is irrelevant for our case ,,maybe I shouldn't have mentioned it, too messy already)

 

[jbriggs444]

(50kg max thrust is not rounding 46 number, I just want to say that this is maximum theoretical thrust when men lean angle is zero degrees(horizontal) so 100kg x 1m =Thrust x 2m...Thrust =50kg but this is irrelevant for our case ,,maybe I shouldn't have mentioned it, too messy already)

OK, now I understand that. It is like hiking out from a sailing boat. You are limited by the length of your legs.

 

[johnrot]

OK, now I understand that. It is like hiking out from a sailing boat. You are limited by the length of your legs.

Yes.

My case with U.J. is very not intuitive/confusing because real external force Thrust at fan is 1,5m above pivot point B but teeter do not rotate clockwise as many would assume at first glance...