Temperature of the Universe based on the ΛCDM Model

[JimJCW]

TL;DR

Let’s plot the temperature of the universe as a function of the cosmological time based on the ΛCDM Model and discuss the results.

Using Jorrie’s calculator we can get the following T vs. t graph up to z = 20,000:

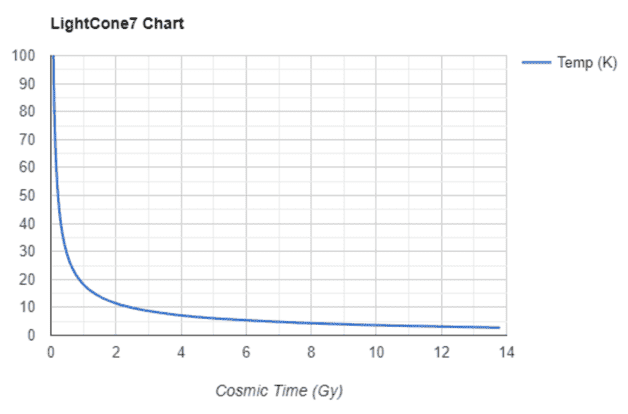
In a log-log plot the above curve is represented by the red solid line in the figure shown below:

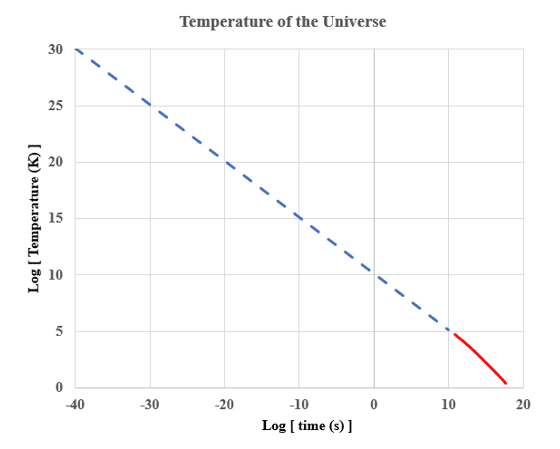
The dashed line shows results for the small a limit using the equation T = 2.725 K / a. Here are some tabulated numbers associated with the above plot:

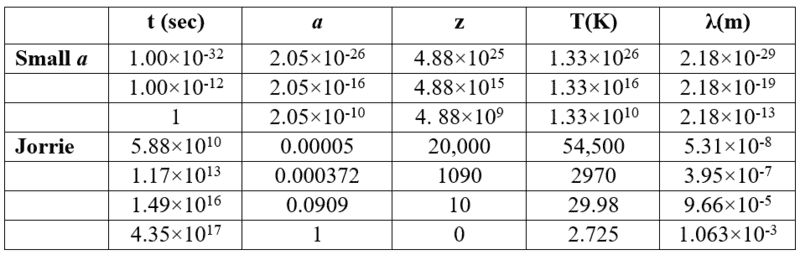
The values of λ are calculated with the equation λ = 1.063 mm × a, based on the peak wavelength of the CMB at the present time.

Note that the above results are qualitatively consistent with the Tabular summary included in the Wikipedia webpage titled Chronology of the universe. According to the estimates in the summary, for t = 1E-12 s, T = 1E15 K and for t = 1 s, T = 1E10 K.

You can help by examining and commenting on the approach given here and see whether it makes sense.

 

[kimbyd]

Did you have a question?

One thing I will say, though, is that the simple scaling of $T \propto 1/a$ is not entirely accurate. It's accurate until you get to a temperature where there was a phase transition where a particular type of particle went non-relativistic. For instance, when electrons/positrons had low enough temperature that all the positrons annihilated, the energy from those positrons got dumped into photons, boosting the temperature of the photon gas.

By contrast, when the temperature got low enough that the weak nuclear force stopped interacting rapidly, meaning that neutrinos stopped interacting much. And those neutrinos didn't pick up the temperature boost from the electron/positron pairs which annihilated later. This has resulted in the cosmic neutrino background today having a slightly lower temperature than the cosmic microwave background (roughly 1.95K vs. 2.726K).

 

[JimJCW]

One thing I will say, though, is that the simple scaling of $T \propto 1/a$ is not entirely accurate. It's accurate until you get to a temperature where there was a phase transition where a particular type of particle went non-relativistic. For instance, when electrons/positrons had low enough temperature that all the positrons annihilated, the energy from those positrons got dumped into photons, boosting the temperature of the photon gas.

By contrast, when the temperature got low enough that the weak nuclear force stopped interacting rapidly, meaning that neutrinos stopped interacting much. And those neutrinos didn't pick up the temperature boost from the electron/positron pairs which annihilated later. This has resulted in the cosmic neutrino background today having a slightly lower temperature than the cosmic microwave background (roughly 1.95K vs. 2.726K).

The following scaling equations are used in our ΛCDM model calculations:

where 1.063 mm is the peak wavelength of the CMB radiation at the present time.

It is a good question to ask whether these equations can be applied to cases of very small a or t. I don’t have enough background to answer it. Hopefully others can.

Let me offer the following two observations:

1. The early universe was radiation dominated, involving a lot of photons. Let’s consider a spherical region of space with a radius of R = 46.5 Gly (current size of the observable universe). It is estimated that there are about 1.5E+89 CMB photons in it. While this number stays about the same, the size of the region was smaller during earlier times, for example, R = 17.3 Mly during the recombination era around t = 0.38 Myr and R = 9.53 ly during the neutrino decoupling era around t = 1 s. My guess is that because the number of photons has been much greater than the number of particles they created, the temperature of the photons has been little affected by the various processes involving the particles. As a result, the above simple scaling equations continue to be valid over time.
2. It is interesting to note that the calculation results discussed in this thread are consistent with T vs. t estimates quoted by others (but I don’t know how the estimates were made): Chronology of the universe and The Early Universe, Toward the Beginning of Time. A demonstration for the latter case is shown below:

 

[kimbyd]

To understand the temperature changes I mentioned, what happens is that at any given time, the energy density for a gas at a temperature T is proportional to $T^4$. That energy density is divided among every relativistic particle species. So if the number of particle species drops because some of them go non-relativistic (and therefore annihilate), then that energy is divided among fewer particle species and the temperature for the remaining species goes up.

This scaling doesn't muck up the graph above because of this $T^4$ scaling: you'd need to multiply the number of relativistic particle species by something like 10,000 to get the scaling off by only one factor of 10. And there simply aren't 10,000 particle types to go relativistic in the first place. So if you're just looking at powers of 10, yes, that scaling graph is fine. This is probably why the first four pairs of numbers in the table above are just powers of ten with no significant digits listed: the details of the physics change those significant digits in complex ways, but the relative power of ten is unaffected.

Bear in mind that the full calculation is more complicated than my explanation here suggests. It's been a while since I looked at these calculations in detail, but you can't simply go "3 particle species (photon, positron, electron) -> 1 particle species (photon)" and get the right answer. It gets you in the right ballpark, but not quite there. And I seem to remember that particle spin plays a role in the calculation as well, but as I said, it's been a while.

 

[JimJCW]

To understand the temperature changes I mentioned, what happens is that at any given time, the energy density for a gas at a temperature T is proportional to $T^4$. That energy density is divided among every relativistic particle species. So if the number of particle species drops because some of them go non-relativistic (and therefore annihilate), then that energy is divided among fewer particle species and the temperature for the remaining species goes up.

This scaling doesn't muck up the graph above because of this $T^4$ scaling: you'd need to multiply the number of relativistic particle species by something like 10,000 to get the scaling off by only one factor of 10. And there simply aren't 10,000 particle types to go relativistic in the first place. So if you're just looking at powers of 10, yes, that scaling graph is fine. This is probably why the first four pairs of numbers in the table above are just powers of ten with no significant digits listed: the details of the physics change those significant digits in complex ways, but the relative power of ten is unaffected.

Bear in mind that the full calculation is more complicated than my explanation here suggests. It's been a while since I looked at these calculations in detail, but you can't simply go "3 particle species (photon, positron, electron) -> 1 particle species (photon)" and get the right answer. It gets you in the right ballpark, but not quite there. And I seem to remember that particle spin plays a role in the calculation as well, but as I said, it's been a while.

Let me first summarize the calculations we have made:

Using the equation,

Jorrie’s calculator can be used to calculate the a vs. t relation up to z = 20,000 (a = 5E-5; t = 5.88E10 s). Together with the scaling equation,

the calculator gives the T vs. t curve shown in the first figure of the thread.

In the small t limit, Eq. (1) becomes (see Friedmann equations),

Together with Eq. (2), this gives the dashed line in the second figure of the thread. As shown by the third figure, the calculation results discussed here are consistent with estimates quoted by others.

Note that a calculator based on Eqs. (2) and (3) is available on the HyperPhysics website to calculate T for a given t with T ≫ 3000 K. The input data there is, however, somewhat different from what we are using here, PLANCK Data (2015).

The ΛCDM model used here cannot possibly describe the early universe in detail; the Radiation Era (see The Early Universe, Toward the Beginning of Time) consists of various epochs such as Planck, Grand Unified Theory, Quark, Lepton, and Nuclear. The question raised by kimbyd is a reasonable one. I don’t have enough background in the field to determine how much the present calculation results is valid for that era.