- #1
Wolfmannm
- 6
- 0
Homework Statement
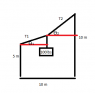
A rope is connected between two fixed points that are separated horizontally from one another by 10 m. The point on the left at a height of 5 m [coordinates (0,5m)], and point on the right is at a height of 10 m [coordinates
(10m,10m)]. A 100 lbs weight hangs from the rope, attached at the location (5m,6m), separating the rope into two segments. What is the tension in each segment? Neglect the weight of the rope. See attached image
Homework Equations
T1 = mg sin ϴ1
T2 = mg sin ϴ2[/B]
The Attempt at a Solution
I fist converted the 100 lb weight to 444.8N. I was thinking that the problem would be similar to one with a horizontal rope with the ends at equal heights, and solved for both ϴ1 and ϴ2 then used these values to calculate the tension in each segment. I got T1 = 87.2 N and T2 = 278.1 N.
Does this seem correct?
Attachments
Last edited: