goldfish9776
- 310
- 1
Homework Statement
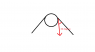
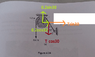
the cord shown have supports a force of 500N and warps over the frictionless pulley , determine the tension in the cord at A and the horizontal and vertical component of reactions at A .
Homework Equations
The Attempt at a Solution
for the moment about A , the author gave 500(0.2) -T(0.2) =0
But if i resolve the T into vertical and horizontal components , my ans would be difrent .. why can't I resolve the forces into 2 components ?
my working :
500(0.2)- Tsin30(0.2) -Tcos30(0.2) = ) , T=386N