SUMMARY
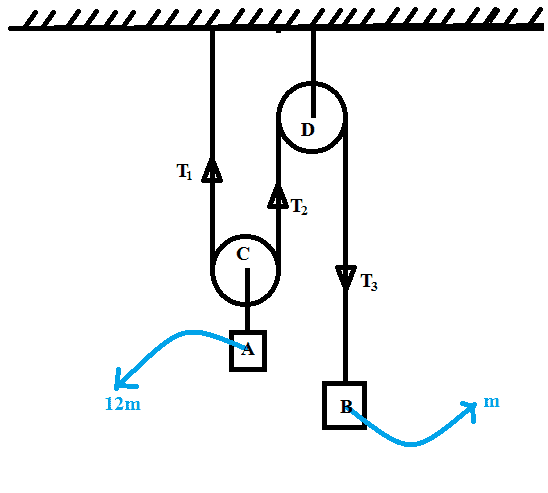
The discussion centers on the behavior of tensions in a frictionless ideal pulley system. It is established that T_1, T_2, and T_3 are equal when the pulleys are frictionless, leading to the conclusion that the tension remains constant throughout the rope. The forces acting on the pulleys are clarified, emphasizing that tensions are not forces but are closely related. Additionally, it is noted that for tensions to remain equal, the pulleys must also be massless, not just frictionless.
PREREQUISITES
- Understanding of basic physics concepts such as tension and force
- Familiarity with free body diagrams
- Knowledge of pulley systems and their mechanics
- Concept of frictionless systems in physics
NEXT STEPS
- Study the principles of tension in different pulley configurations
- Learn about free body diagram techniques for analyzing forces
- Explore the implications of massless versus massive pulleys in mechanics
- Investigate real-world applications of frictionless pulley systems
USEFUL FOR
Physics students, educators, and anyone interested in understanding the mechanics of pulley systems and the principles of tension in physics.