Acceleration of a mass lowered by a motor (Help with Non-Ideal Pulley)

[Kermit_the_Phrog]

Summary: Non - ideal pulley question, should be easy but has got me good

Hey guys, looking for some help on this pulley question. It involves torque, and works with Newton's 2nd law in conjunction with a non-ideal pulley.

Text of question:
" When the motor in the figure below lowers the m = 1160kg mass, it produces a tension of 1.06E+4N in the cable on the right side of the pulley. The pulley has a moment of inertia of 75.7kgm^2 and a radius of 0.747m. The cable rides over the pulley without slipping. Determine the acceleration of the m = 1160kg mass. Use g=9.81m/s^2. "

Diagram:

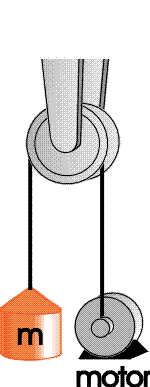
Attempt

I found free body diagrams for both the mass and the pulley, and boiled them down to two equations, two unknowns as follows -

T2 = mg-ma

and

(r^2)T2 - (r^2)T1 = Ia

But when I added the equations together (subbed the first into the second), I got a final answer a = 0.602 m/s^2 , which was wrong.*Note - my final formula was:

a = (r^2)(mg - T1) / (I + (r^2)m)can anyone help me out?

[Moderator's note: Moved from a technical forum and thus no template.]

 

[Kermit_the_Phrog]

But when I added the equations together (subbed the first into the second), I got a final answer a = 0.602 m/s^2 , which was wrong.

So as it Turns out, my answer was correct, BUT my sign was wrong: the correct answer was -0.602 m/s^2.

This makes me more confused honestly.

can anyone help me out explain this?

 

[PhanthomJay]

In your equations, you chose downward and ccw as the positive direction , which is fine , and that’s the way I would have done it. But apparently the solution likes downward to be in the negative direction, per typical convention. But since it was given that the mass is lowered, its picky in my mind to not consider your answer as correct.

 

[Kermit_the_Phrog]

In your equations, you chose downward and ccw as the positive direction , which is fine , and that’s the way I would have done it. But apparently the solution likes downward to be in the negative direction, per typical convention. But since it was given that the mass is lowered, its picky in my mind to not consider your answer as correct.

Thank you very much, it's good to know that I didn't make any sort of fatal error and that the body of my problem solving was okay. I guess the problem was just very picky on those minute details. Have a great rest of your day!

 

[PhanthomJay]

Thank you. You did a very good job in developing your equations. Ribbet, ribbet...