High School Understanding Tensor Indices and Conservation

[etotheipi]

I know what Carroll refers to as 'conservation of indices' is just a trick to help you remember the pattern for transforming upper and lower components, but nonetheless I don't understand what he means in this example:

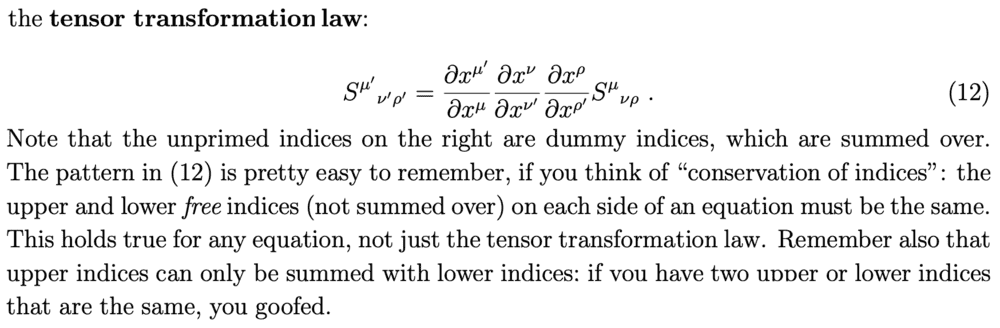
E.g. on the LHS the free index $\nu'$ is a lower index, and on the RHS, the $\nu'$ is an upper index in the denominator of a partial derivative. So maybe I'm missing the point of the heuristic...

 

[vanhees71]

It's correct, though I don't like the notation with primed indices instead of primed symbols. This is utterly confusing and bad notation.

Now concerning the index placement of derivatives. You start with some coordinates $q^{\mu}$. This imply a holonomous basis (of tangent vectors), $\partial_{\mu}$, and dual basis $\mathrm{d} q^{\mu}$.

Now transform to another set of coordinates $\bar{q}^{\mu}$. The dual-basis vectors transform like
$$\mathrm{d} \bar{q}^{\mu} = \mathrm{d} q^{\nu} \frac{\partial \bar{q}^{\mu}}{\partial q^{\nu}},$$
and the basis vectors as
$$\bar{\partial}_{\mu} = \frac{\partial q^{\nu}}{\partial \bar{q}^{\mu}} \partial_{\nu}.$$
As you see the partial derivative wrt. a lower-index object leads to an object with a lower index.

 

[etotheipi]

Thanks! I understand the index placement now, but I'm confused about something else... in what sense do the $\partial_{\mu}$ form a basis, and for what vector space?

 

[weirdoguy]

and for what vector space?

For tangent space. And what do you mean by "in what sense do $\partial_\mu$ form a basis"?

 

[etotheipi]

For tangent space. And what do you mean by "in what sense do $\partial_\mu$ form a basis"?

Ah, okay thanks. He talked a little bit about the tangent space $T_p$ at the beginning, but talked about it having a basis $\hat{e}_{(\mu)}$ and decomposing the vectors in the tangent space like $A = A^{\mu}\hat{e}_{(\mu)}$.

But I've never seen a partial derivative used as a vector before, so I wondered what this is all about... I'm guessing the $\hat{e}_{(\mu)}$ are the $\partial_{\mu}$, but that seems like a pretty strange concept...

 

[weirdoguy]

But I've never seen a partial derivative used as a vector before, so I wondered what this is all about...

Well, tangent vectors can be considered as differential operators acting on smooth functions by means of directional derivative. It's a standard practice to denote basis of tangent space by partial differential operators, since action of those basis vectors on a function gives us partial derivatives of that function. These are standard topics in differential geometry, so I guess it would be a good idea to check some textbook on that for more info.

 

[etotheipi]

That's pretty cool! I searched up the directional derivatives and found an example relating to the velocity components,$$v^i = \frac{dx^i}{dt}$$Then we can consider a directional derivative operator, $\frac{d}{dt}$, along the trajectory $x^i = x^i(t)$,$$\frac{d}{dt} = v^i \partial_i$$Then it's like $\frac{d}{dt} \equiv \vec{v}$, and $\partial_i \equiv \hat{e}_{(i)}$, with the same velocity components $v^i$. A bit weird, but cool...

Thanks, I'll see if I can find some basic stuff on differential geometry

 

[DrGreg]

Thanks, I'll see if I can find some basic stuff on differential geometry

Maybe you've already seen this, but the Wikipedia article on Tangent space discusses several alternative definitions. The relevant subsections for the $\partial_{\mu}$ notation are "Definition via derivations", "Tangent vectors as directional derivatives" and "Basis of the tangent space at a point". And the rest of the article gives more context.

 

[etotheipi]

Maybe you've already seen this, but the Wikipedia article on Tangent space discusses several alternative definitions. The relevant subsections for the $\partial_{\mu}$ notation are "Definition via derivations", "Tangent vectors as directional derivatives" and "Basis of the tangent space at a point". And the rest of the article gives more context.

Thanks! I skimmed those sections and noticed quite a lot of unfamiliar terminology, but I think I could get the gist of it. I'll go through it more carefully tomorrow to unpack it a little more!

Some other notes that I've found that cover the material are on page 31 onward here, and also these notes. The former is a lot more readable as an introduction, whilst I'm struggling more to make sense of the latter. Also I think I should try doing some problems, but the only questions I've been able to find so far are from this document: https://justincfeng.github.io/Tensors_Poor_Man.pdf

 

[vanhees71]

Of course, the abstract notation is more cumbersome than the good old Ricci calculus. Maybe it's good to stick to the latter first. On the other hand the mnemonics for how to transform transform from one holonomic (co-)basis to the other is easier in the abstract calculus.

The most straight-forward source to learn both special and general relativity is Landau and Lifshitz vol. 2 ("Classical Field Theory"). It's the best advanced and most modern text on electromagnetism and gravity I know (though it's written quite a long time ago!). It uses exclusively the Ricci calculus.

To learn the abstract tensor notation, I think Misner, Thorne, Wheeler, Gravitation is great.