Terminal velocity of loop falling through magnetic field

[Rawl]

Homework Statement

https://physicsforums-bernhardtmediall.netdna-ssl.com/data/attachments/72/72755-bc8e4b32405460abcfa2d8e4880f7037.jpg

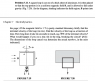
I'm trying to figure out the terminal velocity of the loop as it falls through the magnetic field (figure 7.20).

3. The Attempt at a Solution

The terminal velocity will happen when

$$\vec{F} = 0$$

i.e.

$$mg = \vec{f}_{mag}$$
But we know:

$$\oint \vec{f}_{mag} . d\vec{l} = vBl$$

So

$$\vec{f}_{mag} = vB$$

$$v_t = \frac{mg}{B}$$

Why is this wrong?

 

[Hesch]

You have to regard the energy/power in the system. The square loop has some dimensions which have influence in the resistance, R, of the loop. So as the velocity of the loop increases, the voltage and thus the current will increase, leading to a power loss = I² * R.

This power loss must match the mechanical power supplied = m*g*v.

See the note: The dimensions of the square will cancel out.
It think it's right.