physicsbeginnerss
- 2
- 0
- Homework Statement
- Show, in Figure 4.4, that for a point like P3, x3/y3 > π/2 and for P2, x2/y2 = π/2.
- Relevant Equations
- $$\frac{y1}{x1}>\frac{P2A}{AO}=\frac{2a}{a\pi}=\frac{2}{\pi}$$
This is 'Boas mathematical Methods in the Physical Sciences' homework p484.(Calculus of Variations)
problem2 section4 number 2
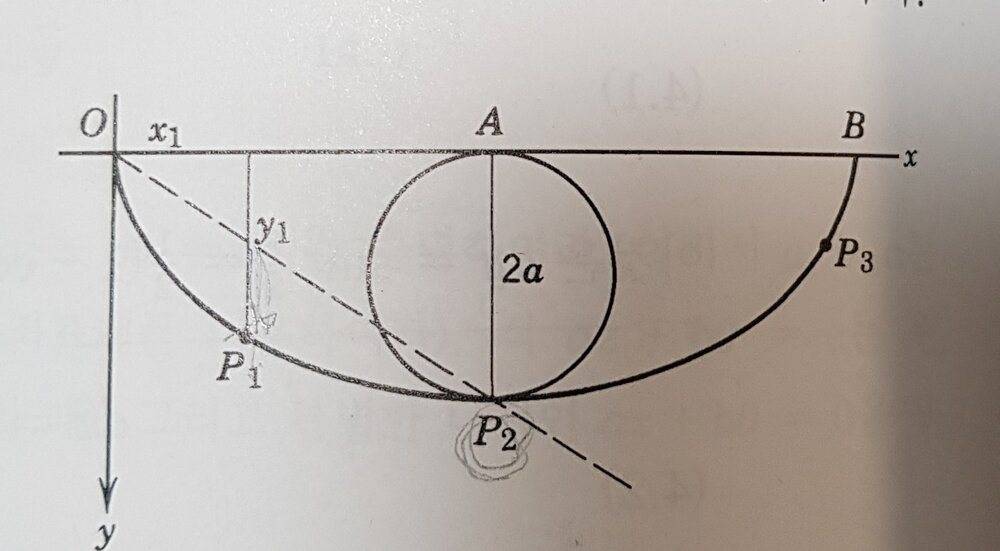
The bead is rolling on the cycloid curve.(Figure 4.4)
And the book explain that
'Then if the right-hand endpoint is (x, y) and the origin is
the left-hand endpoint, we can say that the bead just slides down, or slides down and
back up, depending on whether x/y is less than or greater than π/2 (Problem 2).'
My question is how can be it's just slides down or slides down and back up depending on
the magnitude of x/y? I mean it's depending on potential energy that it back up with origin height.(That contains origin potential energy)
The book explains when it comes to P2 the circle has rolled halfway around so OA=$$\frac{1}{2}\cdot 2a\pi=a\pi$$.
For any point P1 on arc
OP2, P1 is below the line OP2, and the coordinates (x1, y1) of P1 have
$$\frac{y_1}{x_1}>\frac{P2A}{AO}=\frac{2a}{a\pi}=\frac{2}{\pi}$$ or $$x_1/y_1 < π/2$$.
And p3 is applied by same solution that x3/y3 would be greater than $$frac{\pi}{2}$$.
Here is my understanding.
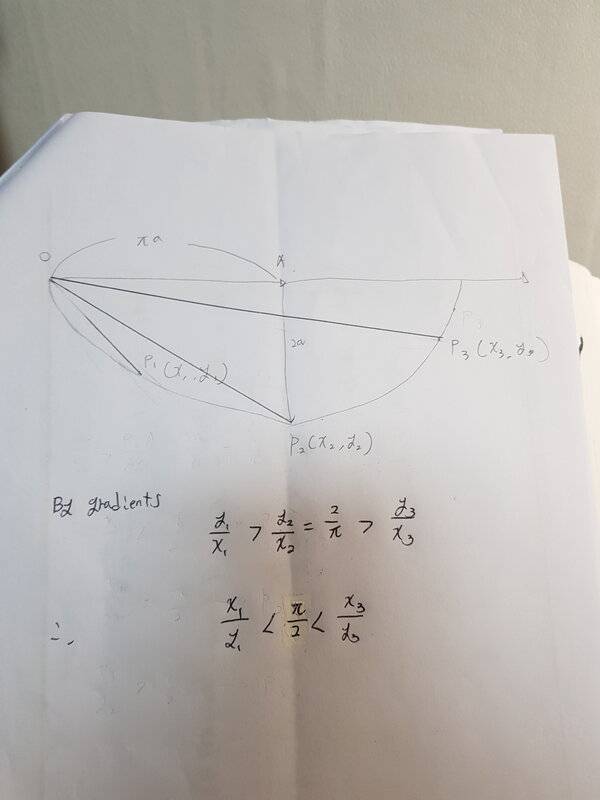
This is what papers says and I drewed it and understand how it works.
But if $$\frac{x_3}{y_3}$$ is less than $$\frac{\pi}{2}$$
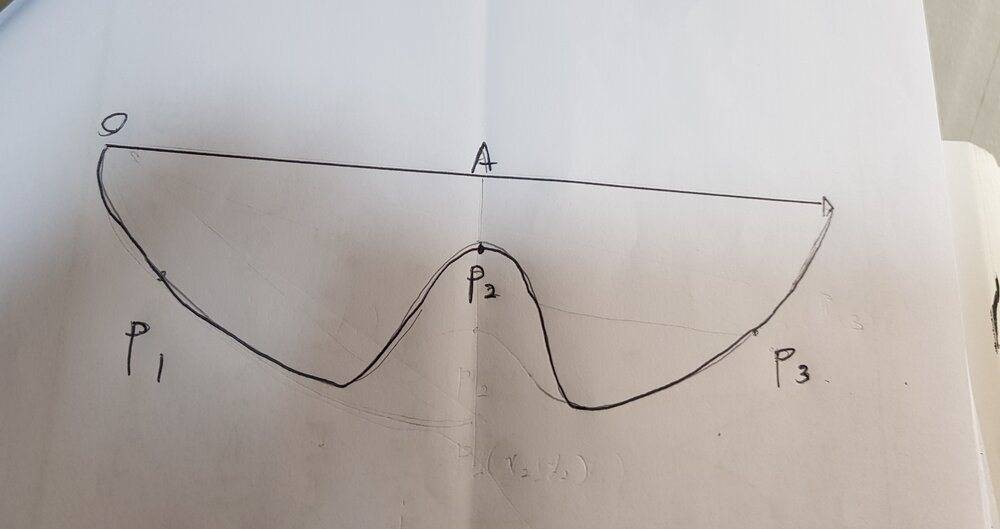
In this curve it's hard for the bead back up to p3, But!, Is this can satified with the parametric equation of cycloid?
## $$x=a(\theta-sin\theta)$$
## $$y=a(1-cos\theta)$$
My question is can the last picture be satisfied with the parametric equation of a cycloid or not? And if not, what is the alternative solution that $$\frac{x_3}{y_3}$$ less than $$\frac{\pi}{2}$$ that is still cycloid curve.
problem2 section4 number 2
The bead is rolling on the cycloid curve.(Figure 4.4)
And the book explain that
'Then if the right-hand endpoint is (x, y) and the origin is
the left-hand endpoint, we can say that the bead just slides down, or slides down and
back up, depending on whether x/y is less than or greater than π/2 (Problem 2).'
My question is how can be it's just slides down or slides down and back up depending on
the magnitude of x/y? I mean it's depending on potential energy that it back up with origin height.(That contains origin potential energy)
The book explains when it comes to P2 the circle has rolled halfway around so OA=$$\frac{1}{2}\cdot 2a\pi=a\pi$$.
For any point P1 on arc
OP2, P1 is below the line OP2, and the coordinates (x1, y1) of P1 have
$$\frac{y_1}{x_1}>\frac{P2A}{AO}=\frac{2a}{a\pi}=\frac{2}{\pi}$$ or $$x_1/y_1 < π/2$$.
And p3 is applied by same solution that x3/y3 would be greater than $$frac{\pi}{2}$$.
Here is my understanding.
This is what papers says and I drewed it and understand how it works.
But if $$\frac{x_3}{y_3}$$ is less than $$\frac{\pi}{2}$$
In this curve it's hard for the bead back up to p3, But!, Is this can satified with the parametric equation of cycloid?
## $$x=a(\theta-sin\theta)$$
## $$y=a(1-cos\theta)$$
My question is can the last picture be satisfied with the parametric equation of a cycloid or not? And if not, what is the alternative solution that $$\frac{x_3}{y_3}$$ less than $$\frac{\pi}{2}$$ that is still cycloid curve.
Attachments
Last edited by a moderator:

