Brachistochrone Definition and 37 Threads

In physics and mathematics, a brachistochrone curve (from Ancient Greek βράχιστος χρόνος (brákhistos khrónos) 'shortest time'), or curve of fastest descent, is the one lying on the plane between a point A and a lower point B, where B is not directly below A, on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696.
The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can only use up to the first half rotation, and always ends at the horizontal. The problem can be solved using tools from the calculus of variations and optimal control.The curve is independent of both the mass of the test body and the local strength of gravity. Only a parameter is chosen so that the curve fits the starting point A and the ending point B. If the body is given an initial velocity at A, or if friction is taken into account, then the curve that minimizes time will differ from the tautochrone curve.

View More On Wikipedia.org
Recent contents Top users
  1. eddiezhang

    Help Understanding A Paper - Brachistochrone With Friction

    Conservation of energy is invoked, which I understand, but the author omits most of the steps. He arrives at (18): I've tried to substitute (13) and (17) into the LHS of the energy conservation equation, but the result is quite messy and my gut feeling is that it doesn't simplify in a nice...
  2. D

    B Verifying AI Chatbot's Answer on Brachistochrone Curve Formula

    I was interviewing an AI chatbot and was wondering how good it is at physics… can anyone confirm whether the answer it gave is true or false? This was through a chatbot called ChatGPT. My prompt: What’s the formula for the Brachistochrone curve? The AI answer: The Brachistochrone curve is a...
  3. D

    Brachistochrone Problem w/ Initial Velocity

    Hello, There is a physics problem called the Brachistochrone problem which I know has been solved for 0 initial velocity (assumes 0 friction and only gravity) and I know the answer is a cycloid. My question is: is there is an existing formula for finding the portion of a cycloid which is the...
  4. physicsbeginnerss

    The Brachistochrone Problem: cycloid curve

    This is 'Boas mathematical Methods in the Physical Sciences' homework p484.(Calculus of Variations) problem2 section4 number 2 The bead is rolling on the cycloid curve.(Figure 4.4) And the book explain that 'Then if the right-hand endpoint is (x, y) and the origin is the left-hand endpoint...
  5. physics_cosmos

    I Solving the Brachistochrone problem with friction

    This Wolfram Alpha Page contains a derivation of the parametric form of the brachistochrone curve that result from either assuming friction or its absence. I am asking for help understanding how the solution to the differential equation obtained from applying the Euler-Lagrange equation to the...
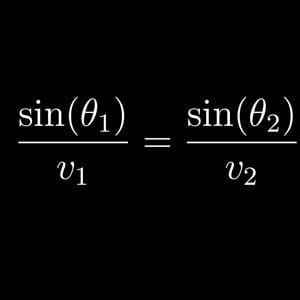
  6. The proof of Snell’s law using springs - 3blue1brown

    The proof of Snell’s law using springs - 3blue1brown

    The law of light bending in matter. Also an important law for the proof of brachistochrone problem.
    • YoungPhysicist
    • Media item
    • brachistochrone refraction snell's law
    • Comments: 0
    • Category: Optics
  7. A

    I Solution to Brachistochrone Problem

    Can anybody post a full solution of the Brachistochrone problem provided by Newton (with full explanations) ? Or, any source about the same would be much helpful. Thank you in advance !
  8. J

    Brachistochrone problem with friction

    Hey, I am doing some research on the brachistochrone problem WITH frictions. I found the following demonstration on the web. The beginning is ok. But I can't understand how the managed to pass between (29) and (30) and between (30) and ((32), (33)). If someone could help me, it would be very...
  9. Joe Wolf

    I Brachistochrone for Specific Ratios

    It is commonly known that the solution to the brachistochrone problem is a cycloid. However, in order for a solution curve to be a cycloid, the ratio between points A on the y-axis and B on the x-axis has to be r/pi*r, since that is the ratio between the "height" of the cycloid and half of its...
  10. Z

    Using Snell's Law for Brachistochrone Project

    Hi all, I'm after a little guidance for I do not know what is going wrong. I understand that for Johann Bernoulli's proof of the brachistochrone problem he used refraction of light and Fermat's principle of least time. I have decided to do a project on the subject, in which I am dividing up a...
  11. zwierz

    I History of brachistochrone and catenary

    Could someone please give me references on historical literature devoted to brachistochrone and catenary problems Thanks.
  12. J

    What are some ways to further explore the brachistochrone problem?

    Homework Statement Hi I'm in second year of study in Math, Physic and Informatic and I require some help. I began a work on the brachistochrone problem. It's really interesting and I already found lot of things (the equation of the cycloid by the Bernoulli's method, I wrote some programs which...
  13. F

    B The Brachistochrone Curve - Which theories apply?

    Hello, I am doing a physics exam, where I have chosen to create a Brachistochrone curve, and perform various tests on it. Furthermore, I also have to write a physics report, containing the theory behind the curve, but I am not 100% sure what some of the theories behind the curve are. I suppose...
  14. wrobel

    Insights General Brachistochrone Problem - Comments

    wrobel submitted a new PF Insights post General Brachistochrone Problem Continue reading the Original PF Insights Post.
  15. Hamza Abbasi

    How Does x in Equation 6.24 Become a(1-cosӨ)?

    Homework Statement This is the solution of Brachistochrone . Homework EquationsThe Attempt at a Solution I am very confused that how the x in equation(6.24) get its value a(1-cosӨ) ? What is the technique behind this solution of x?
  16. rude man

    Insights A brachistochrone subway is not a cost-effective idea - Comments

    rude man submitted a new PF Insights post A Brachistochrone Subway Is Not a Cost-effective Idea Continue reading the Original PF Insights Post.
  17. G

    Brachistochrone. Why a curve at all?

    Why is the solution to the brachistochrone problem a curve at all? If the idea is to get from a higher point to a lower point under the influence of gravity alone, why is a straight line not quicker than a cycloid? It seems counter-intuitive that the shortest time would be along a curve and not...
  18. D

    Optimizing Travel Time: Calculating the Brachistochrone Curve

    Homework Statement I have to calculate minimum travel time between two points. I already have cycloid equations in parametric form: x=r*(t-\sin t) y=r*(1-\cos t) Homework Equations For calculating time i want to use following formula: \int_{0}^{a} \frac{\sqrt{1+{y'}^2}}{\sqrt{2g\,y}}dx My...
  19. B

    Brachistochrone Differential Equation

    The first part of this problem asks me to solve the following for y' : \left( 1 + {y'}^2 \right)y = k^2 So I have: 1 + {y'}^2 = \frac{k^2}{y} {y'}^2 = \frac{k^2}{y} - 1 y' = \sqrt{{\frac{k^2}{y} - 1}} Then I am asked to show that if I introduce the following: y = k^2 \sin^2t Then...
  20. L

    How Is Time Calculated for a Car Sliding Along a Cycloid?

    Homework Statement consider a sigle loop of the cycloid with a fixed value of a. A car is released at a point P0 from rest anywhere on the track between the origin and the lowest point P, that is P0 has a parameter 0<theta0 < pi. show that the time for the cart to roll from P0 to P is given by...
  21. J

    Euler-Lagrange Brachistochrone Problem in rotating system

    Homework Statement Bead slides on a wire (no friction) shaped as r = r(\theta) in the Oxy plane. The Oxy plane and the constraining wire rotate about Oz with \omega = const r, \theta is the rotating polar frame; r, \phi is the stationary frame. Find the trajectory r = r(\phi) in the...
  22. W

    Minimizing the Functional for the Brachistochrone Problem

    Homework Statement So if +x points downward and +y points rightwards then the functional that needs to be minimized is: \sqrt{2g}T[y]=\int_{x_0}^{x_1}\frac{dx}{\sqrt{x}}\sqrt{1+\left(\frac{dy}{dx}\right)^2} Homework Equations I think we just have to use the Euler lagrange...
  23. H

    How Can Friction Be Incorporated into a Brachistochrone Model?

    Hello all, I'm currently an undergrad in my first year doing an experiment with the brachistochrone and I wish to model it mathematically and introduce friction into my model. I understand that the original brachistochrone was solved using the action principle and seems to require Lagrangian...
  24. G

    Brachistochrone with velocity - still a cycloid

    Homework Statement Brachistochrone problem: if the particle is given an initial velocity [tex]v_0 \neq 0[\tex] , show that the path of minimum time is still a cycloid. Homework Equations Conservation of energy: [tex]\frac{1}{2}mv^2-mgy=\frac{1}{2}mv_0^2[\tex] The Attempt at a Solution...
  25. N

    Why Does a Cycloid Curve Minimize Travel Time?

    I am looking for a semi-detailed description of the physics behind the brachistochrone problem. Basically, a brachistochrone is the shape of a ramp that takes the shortest time for a ball to roll down. This shape turns out to be a cycloid. I didn't believe it when I first heard about it, and...
  26. J

    How Do You Solve the Brachistochrone Problem Using Calculus of Variations?

    y[1+(y')^2] = k First solve for dx in terms of y and dy, an then use the substitution y = ksin2(θ) to obtain a parametric form of the solution. The curve turns out to be a cycloid. My attempt: (y')^2 = k/y-1 dy/dx = sqrt(k/y-1) dx = dy/[sqrt(k/y-1)] then substitute y =...
  27. 9

    How do I solve the Brachistochrone Problem with a given differential equation?

    Hello, I'm having problems with a D.E. question, I'm asked to solve the equation: \left(1+y^{'2}\right)y=k^{2} where K is a certain positive integer to be determined later. This more commonly known, as you probably know, as one of the solutions to the Brachistochrone Problem. I really...
  28. T

    Brachistochrone on the surface of a sphere

    1. The problem statement I'm trying to solve the brachistochrone problem between two points on the surface of a sphere. 2. The attempt at a solution The Lagrangian for this problem in spherical coordinates is L=\frac{1}{2}m \left(r^2 \left (\frac{d \theta}{dt}\right)^2+r^2 \sin^2(\theta)...
  29. T

    Brachistochrone homework problem

    1. use the parametric equations of a cycloid ( x=a(t-sint), and y=a(1-cost) ) to show that y=y(x) is the solution of the differential equation for any parameter a. Find the relationship between the radius a in the parametric equations and the constant C in y(1+y`2)=C. 2. Solve the equation...
  30. T

    N.Solve Brachistochrone Homework: Find Time T to Slide Down from Height 0 to -h

    Homework Statement I am after an expression for the time T it takes to slide down from height zero to -h of the brachistochrone. (Starts from x=y=0, slides along a distance -x, descends a height -h). Homework Equations I have deduced that T = \frac{1}{(2g)^{1/2}} \int _{0}^{-h}...
  31. Z

    Centrifugal Potential & Brachistochrone in Polar Coords: Ideas Appreciated

    Anyone familiar with "centrifugal potential" and "brachistochrone" in polar coords? Hi there, The issue appears within this problem: a bead is sliding without friction on a straight wire; the wire rotates in a plane: \omega= const No external fields, no gravity...
  32. E

    Brachistochrone curve - Gravity and other influences

    Homework Statement http://content.answers.com/main/content/wp/en/d/d4/Brachistochrone.png Go to the link and look at this brachistochrone curve. The brachistochrone problem is supposed to find the fastest path between to points for an object under only the influence of gravity, correct...
  33. M

    Brachistochrone Problem/Calculus of Variations

    I'm working on the Brachistochrone probem and I've gotten to the equation: (dy/dx)^2 = (c^2*y)/(1-c^2*y) the 'hint' given is to use y = sin^2(theta)/c^2 to solve the integral. I haven't done any math for 5 months and i haven't been in a pure math class for over a year, so I'm drawing a...
  34. S

    How can the Brachistochrone problem be solved using parametric equations?

    find the curve for which the body will follow such that the time of travel is a minimim. Hints Minimize t_{12} = \int_{x_{1}}^{x_{2}} dt = \int_{x_{1}}^{x_{2}} \frac{ds}{v} = \int_{x_{1}}^{x_{2}} \sqrt{\frac{1+y'^2}{2gy}} dx since F does not depend on x i can use hte beltrami identity (from...
  35. S

    Precursor to brachistochrone problem

    Another long question but not that hard. Most of the writing is my work/questions According to my prof if i cna solve this... the resulting relation can be used to solve Bernoulli's problem For \delta \int_{x_{1}}^{x_{2}} F(x,y(x),\dot{y}(x)) dx = 0 where \dot{y} = \frac{dy}{dx} Show...
  36. H

    How Do You Calculate Time in the Brachistochrone Problem?

    I hope that you've heard about Brachistochrone problem: http://mathworld.wolfram.com/BrachistochroneProblem.html Given two points, I can find (calculate) the courve, on which the ball needs minimum time to travel from point 1 to point 2. I get the equation for the courve, which is cycloid, in...
  37. E

    Integrating the Brachistochrone Problem: Solving for the Optimal Path

    I am gathering my mechanics notes and I put into it some examples. When I get the Hamilton principle I put a section for some basic variation calculus. There's the problem of brachistochrone, I try to solve it, but I get stuck with a integral: the integral that I should make minimal is (I'm...
Back
Top