The Eigenfunction of a 2-electron system

[Settho]

Homework Statement

Show that the wave function is an eigenfunction of the hamiltonian.

Relevant Equations

Hamiltonian, wave function, energy and Born radius

Hello!

I am stuck at the following question:
Show that the wave function is an eigenfunction of the Hamiltonian if the two electrons do not interact, where the Hamiltonian is given as;

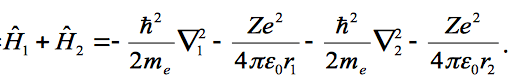
the wave function and given as;

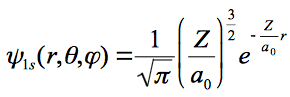
and the energy and Born radius are given as:

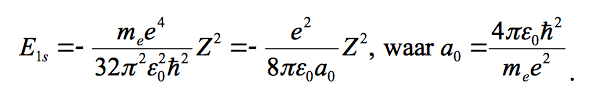
and I used this for ∇ squared:

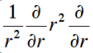
I am stuck at the end of the calculation. I know Z = 2, but somehow I don't end up with the energy, which you need to show that it is indeed an eigenfunction. This is what I get and where I am stuck at:

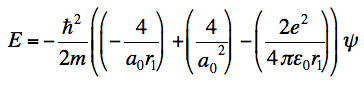
and even when I substitute a0 in this formula, I don't get the energy value. I honestly don't know where it did go wrong.
If someone is able to help, that would be great.

 

[kuruman]

You need to substitute the two-electron wavefunction$$\psi(r_1,r_2)=\psi(r_1)\psi(r_2)=\frac{1}{\sqrt{\pi}}\left( \frac{Z}{a_0}\right)^{3/2}e^{-\frac{Z}{a_0}r_1}\frac{1}{\sqrt{\pi}}\left( \frac{Z}{a_0}\right)^{3/2}e^{-\frac{Z}{a_0}r_2}$$in your Hamiltonian. The energy is a constant and should have no $r$ dependence.

 

[Settho]

But isn't it just the idea to split the Hamiltonian in electron 1 and electron 2 instead of the two-electron wave function?

 

[DrClaude]

I am stuck at the end of the calculation. I know Z = 2, but somehow I don't end up with the energy, which you need to show that it is indeed an eigenfunction. This is what I get and where I am stuck at:
View attachment 242595

The $-\hbar^2 / 2m$ term doesn't factor out of all terms.

 

[Settho]

The $-\hbar^2 / 2m$ term doesn't factor out of all terms.

Your simple suggestion made me solve the problem. Thank you so much!