The inelastic collision between a disk and a rotating platform

In summary, the conversation discusses the conservation of energy in a scenario where a disk is dropped on a rotating platform. The question asks about the final kinetic energy of the platform, and it is explained that energy is not conserved because of the friction between the platform and the disk. It is also mentioned that the work done by friction dissipates mechanical energy into thermal energy, resulting in a decrease in the total mechanical energy of the system.
  • #1
Leo Liu
353
156
Homework Statement
A FR question in 2019 AP Physics C Exam (Version 2)
Relevant Equations
Rotational Kinetic Energy, Conservation of Angular Momentum
A disk is dropped on a platform rotating at a constant angular speed ##\omega_i## as shown below.
1588882549551.png

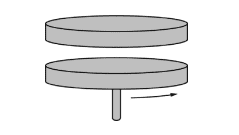
The question asks whether the final kinetic energy of the platform is conserved. I understand the angular momentum is always conserved provided that the net torque is 0, so I wrote the following equation:
$$I_{platform} \omega_i = (I_{platform}+I_{disk}) \omega_f$$
From this I inferred that ##\frac 1 2 I_{platform} {\omega_i}^2 \neq \frac 1 2 (I_{platform}+I_{disk}) {\omega_f}^2##.

My questions are as follows: Why is the energy not conserved in the collision, and how is the energy dissipated?

Thank you in advance.
 

Attachments

  • 1588882478810.png
    1588882478810.png
    14.5 KB · Views: 116
  • 1588883047773.png
    1588883047773.png
    19.3 KB · Views: 100
Last edited:
Physics news on Phys.org
  • #2
What force must act between the platform and the disk in order to equalise their angular velocities? Does this force dissipate mechanical energy into anything else?
 
  • #3
etotheipi said:
What force must act between the platform and the disk in order to equalise their angular velocities? Does this force dissipate mechanical energy into anything else?
I think it's kinetic friction because the angular speed of the platform decreases as the rotation of the disk speeds up. Am I right?
 
  • #4
Leo Liu said:
I think it's kinetic friction because the angular speed of the platform decreases as the rotation of the disk speeds up. Am I right?

Yes that's right.

And friction dissipates mechanical energy into thermal energy. Actually, the total work done by friction at the interface, ##W##, is the change in mechanical energy of the system. The change in thermal energy of the system is ##-W##. Energy is conserved... just not KE!
 
  • Like
Likes Leo Liu

FAQ: The inelastic collision between a disk and a rotating platform

What is an inelastic collision?

An inelastic collision is a type of collision where the kinetic energy of the system is not conserved. This means that the total energy of the system before and after the collision is not the same. In an inelastic collision, some of the kinetic energy is converted into other forms of energy, such as heat or sound.

What is the difference between an inelastic collision and an elastic collision?

In an elastic collision, the total kinetic energy of the system is conserved. This means that the total energy of the system before and after the collision is the same. In an inelastic collision, some of the kinetic energy is lost, while in an elastic collision, all of the kinetic energy is conserved.

How does a disk colliding with a rotating platform result in an inelastic collision?

When a disk collides with a rotating platform, some of the kinetic energy of the disk is converted into rotational energy of the platform. This results in a loss of kinetic energy, making the collision inelastic.

What factors affect the outcome of an inelastic collision between a disk and a rotating platform?

The outcome of an inelastic collision between a disk and a rotating platform can be affected by factors such as the mass and velocity of the disk, the rotational speed of the platform, and the angle at which the disk collides with the platform. Other factors, such as the materials and surface properties of the disk and platform, can also play a role.

How is the conservation of momentum applied in an inelastic collision between a disk and a rotating platform?

The law of conservation of momentum states that the total momentum of a system remains constant before and after a collision. In an inelastic collision between a disk and a rotating platform, the total momentum of the system is conserved, but the kinetic energy is not. This means that the final momentum of the system is equal to the initial momentum, but the final kinetic energy is less than the initial kinetic energy.

Similar threads

Perfectly inelastic collision between Projectile and a hinged disk
Replies
26
Views
615
What is the final angular displacement of a disk hit by two masses?
Replies
3
Views
1K
Question about the current components inside the Corbino disk
Replies
11
Views
571
Conservation of Energy and Angular Momentum in a Rotating Train-Disk System
Replies
30
Views
3K
Perfectly inelastic collision of two moving and rotating disks
Replies
9
Views
2K
Rod swinging and hitting a ball
Replies
31
Views
3K
Why can we use this approximation in rotational work-kinetic energy theorem for small displacements?
Replies
7
Views
783
Angular momentum after a collision
Replies
1
Views
1K
MIT OCW 8.01 PS11.3: Elastic Collision Between Ball and Pivoted Rod
Replies
10
Views
1K
Avg Power in a Rotational Energy/Work Problem
Replies
6
Views
756

Hot Threads

Recent Insights

Back
Top