- #1
dcmf
- 16
- 5
- Homework Statement
- Consider a motor that exerts a constant torque of 25.0 N⋅m to a horizontal platform whose moment of inertia is 50.0 kg⋅m^2. Assume that the platform is initially at rest and the torque is applied for 12.0 rotations. Neglect friction.
What is the average power Pavg delivered by the motor in the situation above? Enter your answer in watts to three significant figures.
- Relevant Equations
- K = (1/2)Iw^2
W = τΔθ
P = W/Δt
This question has multiple parts and according to all the work done up to this point...
Now I'm being asked...
I assumed to find average power I would need average work, especially because the question's hint prompted me to find the average angular velocity, which it confirmed to be 4.34 rad/s. So I did the following calculations:
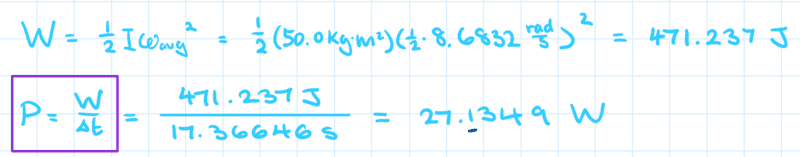
27.1 W was not accepted as the answer. Any advice on adjustments to make to my equation? Is there a rounding error?
How much work W does the motor do on the platform during this process?
1885 J
What is the rotational kinetic energy of the platform Krot,f at the end of the process described above?
1885 J
What is the angular velocity ωf of the platform at the end of this process?
8.68 rad/s
How long Δt does it take for the motor to do the work done on the platform calculated in Part A?
17.4 s
Now I'm being asked...
What is the average power Pavg delivered by the motor in the situation above?
???
I assumed to find average power I would need average work, especially because the question's hint prompted me to find the average angular velocity, which it confirmed to be 4.34 rad/s. So I did the following calculations:
27.1 W was not accepted as the answer. Any advice on adjustments to make to my equation? Is there a rounding error?