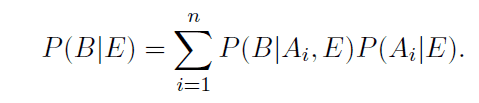SUMMARY
The discussion centers on the law of total probability with extra conditioning, specifically addressing the need for the events \(A_i\) to form a partition of the sample space \(E\). Participants clarify that when all probabilities are conditional on \(E\), it simplifies the equation, treating \(E\) as the universal set. The proof hinges on ensuring that the \(A_i\) events partition \(E\) correctly, which is essential for applying the theorem accurately.
PREREQUISITES
- Understanding of probability theory fundamentals
- Familiarity with conditional probabilities
- Knowledge of event partitioning in probability
- Basic proof techniques in mathematics
NEXT STEPS
- Study the formal statement of the law of total probability
- Learn about event partitioning and its implications in probability
- Explore conditional probability and its applications
- Review mathematical proof strategies in probability theory
USEFUL FOR
Students of probability theory, mathematicians, and anyone seeking to deepen their understanding of conditional probabilities and the law of total probability.