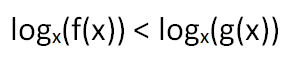The Limited Logarithm: Why x Can't Be <= 0

  • Context: MHB 
  • Thread starter Thread starter roni1
  • Start date Start date
  • Tags Tags
    Logarithm
Click For Summary
SUMMARY

The discussion clarifies that logarithms are only defined for positive bases due to the mathematical implications of exponentiation. Specifically, the equation P = log_x(Q) translates to Q = x^P, which presents undefined scenarios when x is less than or equal to zero. For instance, defining x^{-1} when x equals 0 or x^{1/2} when x equals -1 leads to contradictions, necessitating the restriction of logarithmic functions to positive bases only.

PREREQUISITES
  • Understanding of logarithmic functions
  • Familiarity with exponentiation principles
  • Basic knowledge of mathematical definitions and properties
  • Concept of undefined mathematical expressions
NEXT STEPS
  • Study the properties of logarithms with positive bases
  • Explore the implications of exponentiation with negative and zero bases
  • Learn about complex logarithms and their definitions
  • Investigate mathematical conventions for undefined expressions
USEFUL FOR

Mathematicians, educators, students studying algebra, and anyone interested in the foundational principles of logarithmic functions.

roni1
Messages
20
Reaction score
0
Why x can't be less or equal to zero?
 

Attachments

  • inequality.png
    inequality.png
    1.1 KB · Views: 105
Mathematics news on Phys.org
roni said:
Why x can't be less or equal to zero?
P= log_x(Q) is equivalent to Q= x^P. How, exactly, would you define x^{-1} if x were equal to 0? How would you define x^{1/2} if x were -1? In order that we not have to give special definitions to cases like those, we only define the exponential for positive base. And from that, logarithm can only be defined for positive base.
 

Similar threads

High School Issue With Algebra of Logarithms
  • · Replies 8 ·
Replies
8
Views
2K
High School Logarithmic Function: Can Domain of Logarithm be R?
  • · Replies 11 ·
Replies
11
Views
2K
MHB How do I Solve a Basic Logarithm Problem?
  • · Replies 5 ·
Replies
5
Views
2K
Logarithmic Regression Question (TI-84 Plus Graphing Calculator)
  • · Replies 4 ·
Replies
4
Views
2K
High School Are Logarithms Useless? Why Need them Given Exponents?
  • · Replies 12 ·
Replies
12
Views
3K
Undergrad How to solve for X in engineering economy problems involving annuities?
  • · Replies 17 ·
Replies
17
Views
3K
High School Plotting the Solar System's planets' distances logarithmically
  • · Replies 17 ·
Replies
17
Views
3K
MHB Is this Trigonometric Expression a Constant Function of x?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Solving Logarithmic Equations: Expert Help with Different Bases
  • · Replies 4 ·
Replies
4
Views
2K
MHB Triangle and logarithm problem
  • · Replies 5 ·
Replies
5
Views
2K