The Mystery of Center of Gravity (CoG) and Center of Mass (CoM)

[Lisciu]

Hello everyone,

Since yesterday I'm struggling with concept of CoG and of course in CoM.

The problem is that I don't understand why lower to the ground CoG is more stable then CoG more off the ground. On the internet there is batch of information about that but nobody explained it by momentum equlibrium. And that's what I need to understand that because of course i feel that but when i trying to do moments of equilibrium then i don't see this dependence.

For example two drawings:

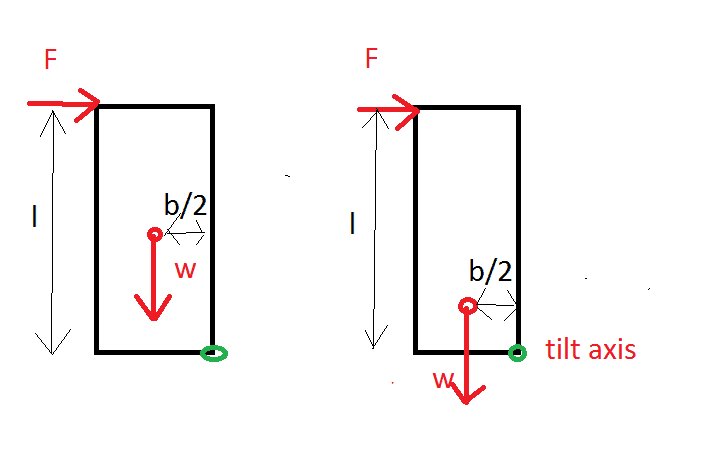
From the Moments around the point called "Tilt axis" I compute the equation:

Fl = Wb/2 in both case and I see the depend on the base rather then position of CoG. Can someone explain my what I do wrong? Should I point the force that i attached as a pulling one to the CoG? But it will make no sense from my point because it's like open a door lever task. If i will need to move the force to CoG i will generate less moment and door shouldn't open.

It's make my head blow up. Could someone help me to understand where is mistake?

I also trying to understand why we put sometimes force (not only the weight of itself) in CoG and when we should?

 

[DEvens]

Um... What is it you are trying to calculate? You have a force. Is that the only thing you need to know in order to know stability?

Consider how far the force must act to get the block to tip over. Consider this as a function of the height above the floor the CoG is located.

Consider giving the block a smack. That is, impart an impulse. How much impulse would you need to impart to get the block to tip over with the CoG at different heights above the floor?

 

[Lisciu]

Dear Mr DEvens,

Honestly I trying only to find why stability of something depends on height of CoG. I know about leverage, opening doors etc. and i totally get it. But thing i don't know is how it works in math way in case of this box. Because when I take the moment force around the tip point, then i don't have in moment arm the height for Weight of the block. So it's hard to understand why it actually depends on the position of CoG.

 

[DEvens]

Dear Mr DEvens,

Honestly I trying only to find why stability of something depends on height of CoG. I know about leverage, opening doors etc. and i totally get it. But thing i don't know is how it works in math way in case of this box. Because when I take the moment force around the tip point, then i don't have in moment arm the height for Weight of the block. So it's hard to understand why it actually depends on the position of CoG.

So, you answered my questions? What were the answers?

 

[Lisciu]

1. I don't think I need something more. If you mean the friction i want to neglected this case and keep it simple. Even with friction there will be no arm as a height of force from CoG. In my example the height of the box is important not the height of CoG and that is the problem.

2. I don't want to go to dynamics with this. Just simple statics.

I am not a physics guy so apologize if I don't understand you.

 

[DEvens]

Sigh. Ok, under what circumstances will the block tip over? What exactly has to happen for the block to tip over? And how does that change when the height of the CoG above ground changes?

To be as blunt as I am going to be, where will the CoG be relative to the corner you have called "tilt axis" when the block starts to fall over?

 

[Nidum]

Try re-drawing the diagrams with the two blocks tilted so that their centres of gravity are vertically above the pivot points .

Update : D.Evans is saying same thing - I missed by a button press !

 

[Lisciu]

The force of pulling need to be larger then moment from the weight. And it will going to fall when the CoG will be further then tilt axis. But still I don't understand this...

 

[DEvens]

The force of pulling need to be larger then moment from the weight. And it will going to fall when the CoG will be further then tilt axis. But still I don't understand this...

So how far does the CoG have to move to be over the tilt axis? And does this depend on how far it is from the floor? And how does it affect motion of the block?

Draw the picture with different height CoG. How far does the block rotate with a high CoG compared to a low CoG?

 

[Lisciu]

It's travel more where the CoG is lower and of course I knew that. But i don't now why from vector and analytical way. But why it will fell down when the CoG get further then axis of tilt?

 

[DEvens]

Your diagrams are not very good. You have the same angle for both. And you have the CoG past the corner in both cases. It will be a different angle with a different height above the floor.

How much must the CoG move *UPWARDS* in each case? And what does that mean about *ENERGY*? Stability is a dynamic thing.

 

[SteamKing]

It's travel more where the CoG is lower and of course I knew that. But i don't now why from vector and analytical way. But why it will fell down when the CoG get further then axis of tilt?

Once the CoG moves to the right of the green circle as the box is tilted, the box will fall over clockwise unless restrained by another force acting to the left.

The higher the location of the CoG is above the base of the box, the less tilting you need to topple the box over. This is why we say that a high CoG makes things less stable. (This works with botes, too, not just boxes.)

 

[PhanthomJay]

2. I don't want to go to dynamics with this. Just simple statics.
.

But simple statics won't give you the answer, because regardless of the height of the CoG, as long as it is the same distance horizontally from the tilt axis, it takes the same force to cause the object to be on the verge of tilting about the lower corner. So for any force F up to a limiting value, the object is at rest, that is , the sum of forces (including the weight, force F, and the normal force) and sum of torques about the pivot(including torque from the normal force, which shifts from center to corner as the load increases ) is 0.
Now when the applied force exceeds the static limit, that is, when it exceeds Wb/2l, now the box is unstable and starts to tilt and rotate and angularly accelerate. The previous responses explain why then the height of the cg becomes important in keeping the cg left of the tilt axis until release of the applied force.