The relation between entropy and probability at quantum levelu

[mitchell porter]

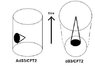
Well, let's just look more closely at the mapping from that paper, a mapping from a region on the boundary to a point in the bulk. Mathematically, it's defined on page 3, equation 2.4. Also see slide 10 from http://www.phys.vt.edu/~sowers/talks/kabat.pdf" .

In both references, the equation describes the field at a point in anti de Sitter space, but the picture is of a point in de Sitter space. In the picture of de Sitter space, time is in the vertical direction, so it's saying that the boundary is in the past. The "smearing", which defines the region on the boundary which maps to the point, is in two space directions on the boundary (I'm referring to the circle at the base of the light cone in the picture).

In the equation, which is for anti de Sitter space, we are defining "phi" in the bulk in terms of "phi0" on the boundary. You'll see that phi depends on three coordinates, T, bold X, and Z; but phi0 just depends on T and X. T is time (on the boundary or in the bulk), bold X is a vector (which is why it's printed in bold) and represents the space coordinates on the boundary, and Z is the extra space dimension in the bulk. So we're constructing something at a point in the bulk (with coordinates T, X, and Z) as an integral over a region on the boundary (ranging over values of T and X).

Now look at the phi0 term that we are integrating over. You'll see that time ranges over T+T', while space ranges over X+iY'. Both T' and Y' are real numbers that range over positive and negative values, and represent points on the boundary away from (T,X,0) - that is, away from the (T,X) point on the boundary where the bulk coordinate Z is just 0. So when T' is negative, it's back in time, when T' is positive, it's forward in time. But we're adding iY' to X; the boundary coordinates are supposed to become complex numbers. What does that mean?

In calculus, it's very common, when solving an equation for real numbers, to switch to complex numbers first, where it is often easier to solve, and then to later return just to real numbers. But here there is actually a physical meaning too.

In relativity, there's a formula for the length of the http://en.wikipedia.org/wiki/Spacetime#Basic_concepts" between two points. The square of the length is negative for timelike separation, positive for spacelike separation, and zero for lightlike separation. "Timelike separation" means that one point is definitely (causally) in the future of the other point. Because of the way that space and time change in relativity, when viewed from different reference frames, sometimes A can be in the future of B, in one frame, but in its past in another frame. So you can't just use the time coordinate to determine the ordering of events. If A is, not just in the future of B according to the coordinate system, but also close enough to B in space that it is in the "future light cone" of B, then it is definitely in the future of B, there's no physically valid coordinate change which will put it into the past. Timelike separation refers to this relationship of definitely being in the future. Something that is spacelike separated, you could think of as "quasi-simultaneous". There will be coordinate systems where it's in the future, others where it's in the past, but it's always too far away for a causal connection at the speed of light.

These are the basics of special relativity. Now notice, just as a fact of algebra, that if you could somehow have something which was an imaginary-number amount of time into the future, the square of the spacetime interval would now be positive, even though timelike is supposed to be negative, because the i factor in the interval length would produce an extra factor of -1 in the square of the length.

It is also a fact that de Sitter space and anti de Sitter space are closely connected geometrically. I wrote a little about it https://www.physicsforums.com/showthread.php?p=3222927". You can get both spaces from the same geometric object, but choosing a different direction for time.

So, returning to the paper: their region-on-the-boundary-to-point-in-the-bulk map for anti de Sitter space is an analytic continuation of the region-on-the-past-boundary-to-point-in-the-present-bulk map for de Sitter space. More precisely, they use a formula which makes sense in de Sitter space, because all the space and time distances in the formula are specified in real numbers, and then they transform that into a formula which looks like the anti de Sitter formula by making some quantities imaginary. So the resulting formula is a peculiar intermediate thing: it's motivated by how de Sitter space works, but it's applied in anti de Sitter space, but it relies on treating coordinates in anti de Sitter space as if they were complex numbers rather than real numbers. (Among other things, that would double the number of real dimensions, because now you have x+yi wherever you previously just had an x.)

Most physicists are rather unconcerned about formal manipulations like this, because they are just intermediate steps in a larger calculation. For example, you might be computing the probabilities of various outcomes of a particle collision in which the motion of the incoming particles are specified by momentum vectors. Those probabilities will be complicated functions of the momentum vectors. It is an utterly routine thing for such functions to be computed by treating the momentum vectors as vectors of complex numbers, and then later restricting back to real numbers in some way. The same thing happens here with the "complexified boundary" coordinates. We are actually talking about fields whose value varies across space and time in a way that depends on space-time coordinates, so using complex-valued space-time coordinates really means, using complex numbers as an input to the function which defines how the field varies with space and time. In this case, we are then figuring out something about the value of the field at a point in the bulk - a point whose coordinates are definitely just real numbers - by an integration over the behavior of the field on the complexified boundary.

According to the usual pragmatic philosophy, we don't care too much about the implicit doubling of dimensions on the boundary that this involves, because that's just an intermediate step. What we start out with is a specification of how the field behaves on the boundary, we mysteriously extend that specification to "the way the field would behave if the boundary coordinates were complex numbers rather than real numbers", we perform a big integral, and since we get an answer which once again involves just real-valued coordinates, we don't have to worry about whether the complex-valued space-time coordinates correspond to something real.

But if we want to invert this mapping, we're trying to go from a region in the bulk to a point on the boundary. Therefore, we either have to go back to the uncomplexified boundary, or we have to start taking the complexified boundary literally.

Earlier in this thread I mentioned Roger Penrose's twistors. They also derive from a complexification of space-time coordinates. But Penrose, at least, wanted to consider them as a fundamental theory (most of the people now using twistors regard them just as a mathematical tool). So maybe, if we want to map bulk nonlocality to boundary locality, we have to use twistors somehow. And there's the fact that the "third theory" of Arkani-Hamed et al, which adds a third description to the bulk/boundary duality, is expressed in terms of twistors. The only problem is, I don't think twistors look local in terms of the boundary either (at least, not in terms of the usual boundary, with real-only coordinates). So if we're chasing after the origins of quantum mechanics itself, this may be an indication that seeking classical locality on the boundary is not the answer - that the boundary will remain quantum. And after all, that's how it is in the orthodox use of AdS/CFT.

 

[mitchell porter]

However, having said all that, let me mention one thought arising from your comments on Mongan's paper. I complained that I didn't see how Mongan wanted his boundary to provide boundary conditions to quantum wavefunctions in the bulk. But the stipulation that the boundary should be local in the classical sense - that you can describe it reductionistically, in terms of states confined to the "pixels of surface area" - could perhaps be expressed in quantum terms, as a requirement that the wavefunction on the boundary can be factorized into local states. In other words, no entanglement, it's just a tensor product of wavefunctions on the "pixels". If you could define a Schrodinger equation for evolution of a bulk wavefunction, whose restriction to the boundary remained factorized in this way, maybe you'd be getting somewhere; but I don't think this would resemble the concrete examples of gauge/gravity holography that have been discovered so far, because the dynamics of the boundary theory should produce entanglement on the boundary in all such cases.

Smolin's copy dynamics has the problem, which he mentions in his section VI, that there's no rule governing the dynamics of a hierarchy of composite systems. A molecule contains an atom contains a proton: does the proton copy its state from another proton, or does the whole atom copy its state from another whole atom, overriding the proton's copy dynamics? To understand how the holographic dynamics of nested systems works, it might be better to obtain guidance from a worked example in AdS/CFT, if we can find one.

edit: I said

I don't think this would resemble the concrete examples of gauge/gravity holography that have been discovered so far, because the dynamics of the boundary theory should produce entanglement on the boundary in all such cases.

But if we suppose that the version of dS/CFT that is relevant for the real world involves past and future boundaries, maybe this doesn't matter, because the boundary theory has no dynamics! In this version of dS/CFT, the time direction is the bulk - space-time holographically emerges from a boundary which is purely spatial.

However, we may end up finding out that, even though the boundary here has no dynamics, it still requires an entangled quantum state on the boundary to give rise holographically to quantum dynamics over time in the bulk.

 

[dhillonv10]

mitchell, thanks for that post, I haven't studied the local nature of twistors for the boundary before so I'll look around, study and then come back to address the concerns you mentioned, and it may be as you said, the boundary remains quantum.

Another observation, this one however may not be that relevant, I just saw another paper: Constructing local bulk observables in interacting AdS/CFT (I think this was mentioned here before, the problem again is that it is in AdS)

6.2 Bulk Feynman diagrams

In this section we show how the Feynman diagrams associated with a local theory in the bulk can be mapped over to CFT calculations. This will provide yet another way of deriving the CFT operators which are dual to local bulk observables.

Although in the mean time, regarding this paper: A new twist on dS/CFT, http://arxiv.org/abs/hep-th/0312282" I emailed one of the authors to ask about the point brought up at pg. 7

edit #2: Also see page 7 here for a boundary-to-bulk map for de Sitter space.

Here's the whole email:

Vikram Dhillon, <Thu, Jun 9, 2011 at 1:30 AM>
To: lowe@brown.edu

Hi Prof. Lowe,

I recently came across your paper on A new twist on dS/CFT and on page 7
you mention a mapping from boundary to bulk by promoting the modes on
the circle to the modes on the de Sitter. I have a question about that,
is it possible to formulate an inverse of this mapping? Can the inverse
of this mapping be written down where we have a function mapping
bulk-to-boundary in dS/CFT? Thanks for your time.

- Vikram


David Lowe <david_lowe@brown.edu> Thu, Jun 9, 2011 at 4:36 PM
To: Vikram Dhillon 

Yes, the inverse map is easier -- you just look at the asymptotics of
the bulk mode near infinity (I think we had in mind past infinity),
and extract the appropriate coefficient of the time dependent piece.
If the bulk mode is a positive frequency mode with respect to the
Euclidean vacuum, this time dependent factor should be uniquely
defined.

I don't fully understand what he is stating in the email, mostly because I haven't read that paper but this email shows that it is possible to construct an inverse mapping. This case isn't similar to what we were discussing before mostly because in the other paper they focused on an AdS space and then mentioned the local buk operators, this new approach, if it works, is more direct now that we are focusing on the dS space.

Now my question with this post is that, say for instance, we are able to construct a mapping from bulk-to-boundary, then how would that show the holographic transformation of boundary locality to bulk nonlocality? and that also raises the concern if the boundary is local at all.

 

[dhillonv10]

Actually I think I can somewhat answer my question, please correct me where needed, ds/CFT correspondence implies the duality between the bulk and boundary, the mapping will show, when two points, that are far away interact, that interaction (through the use of the constructed mapping) is actually occurring between those points locally.

 

[mitchell porter]

Here we are talking about a free (non-interacting) http://en.wikipedia.org/wiki/Scalar_field" , you can see that space in dS2 is just a circle (time runs vertically, up the hyperboloid surface in the diagram).

In Fourier analysis, you can express an arbitrary oscillating curve as a weighted sum of periodic curves, the Fourier modes. You can do the same thing http://www.flickr.com/photos/ethanhein/2680541012/" . So classically, the behavior of this free field just consists of the waves in each of its component modes, moving around the circle. On the diagram, if you followed just one peak in one mode, you would see it trying to trace out a spiral up the diagram (movement around the circle in space translates to movement in an upward spiral on the space-time diagram); but the accelerating expansion of dS2 (represented by the vertical spreading out of the hyperboloid) would outrun it, so that it never got any further than halfway around the circle. Since we are talking about a quantum field, we also have to talk in terms of probabilities, but since it's a free field, the probabilities for each mode are independent, so it's not too complicated (compared to interacting fields).

If you look at the bottom of the picture of dS2, you'll see space is a circle (horizontal cross-section of the hyperboloid), just as it is at every other time in this coordinate system, infinitely far into the past or the future. So the dS2 space-time theoretically extends infinitely far into the past, and this allows us to define a "circle at time = -infinity". This is the "past infinity" to which David Lowe refers. We can also extrapolate the behavior of the field modes endlessly back in time - this is their asymptotic behavior at past infinity. For example, if the activity in one field mode just subsides to zero, it asymptotes to zero. But if the mode just oscillates endlessly as you extrapolate it back, it doesn't converge to anything. However, you may still be able to say something about its asymptotic behavior - for example, that the size of the oscillations approaches a constant. This is the time-dependent piece of the asymptotic behavior.

For the final detail, we have to remember we are talking about quantum field modes, so we are talking about probabilities (which may be expressed in terms of "correlation functions"). So really we're extrapolating the quantum correlation functions for the scalar field modes endlessly back in time, and this gives us correlation functions for the scalar field "at past infinity". Here is where the holographic magic happens: we re-express the correlation functions at past infinity in terms of correlation functions for "conformal primary operators" on the circle at infinity, and then we discover that these conformal operators also gives us a language for talking about dS2 correlation functions at any point in the history of dS2, not just at past infinity. These operators are built from "conformal fields" which are defined to exist only on the circle at past infinity, but which allows us to extrapolate the behavior of the scalar field at any time and place in space-time (in the diagram, that's any time and place on the hyperboloid surface).

To extend this construction to higher dimensions, the boundary at past infinity would be a sphere or a hypersphere (e.g. the past boundary of dS3 would be the surface of an ordinary sphere, the past boundary of dS4 would be "S^3", a hypersphere), and we would start with Fourier modes in multidimensional space, not just on a circle. Also, it needs to be done for other types of field (spinor, vector, tensor) and for interactions between fields.

 

[mitchell porter]

This is about as simple a prototype of dS/CFT as we are likely to find, so we should try to understand it in detail. One thing to understand is that the mapping between modes on de Sitter and "modes on the circle" is only halfway to the full holographic correspondence; it's just the extrapolation of the bulk field's behavior back to past infinity. The real heart of the correspondence is the re-expression of the bulk correlation functions at past infinity, in terms of CFT operators. The CFT is the boundary theory, a completely different set of fields which nonetheless implicitly contain all the information about how the fields in the future "bulk" will behave.

With respect to locality and nonlocality, a description in terms of Fourier coefficients is about as nonlocal as you can get: instead of stating the value of the scalar field at a particular point on the circle, instead you state the strength of all the different modes stretching around the circle - and if you do the resulting Fourier sum at that point, you get back the field strength at that point. But the correlation functions on the boundary can easily be re-expressed in terms of position rather than mode strength - see the sentence under equation 13 in "A new twist on dS/CFT", which refers to "delta(theta'-theta) in coordinate space". Delta functions like that equal 1 if the two variables are the same, and equal 0 otherwise, so what that seems to be saying is that nothing at past infinity can move (probability for propagation equals zero, if the particle has to move from one location on the circle, theta, to a different location, theta') - which makes some sense if you think about the nature of de Sitter space; space itself expands so quickly that every particle eventually gets turned into an island, unable to reach its neighbors. Asymptotically (at infinite time), any surviving matter is stuck in its own patch of space, which will shrink to a point on the circle at infinity.

Since there's no time in the CFT here, it seems like we will just start with entanglement of the conformal fields around the circle (or across the (hyper)sphere, for higher-dimensional dS), and then, with the holographic emergence of a time dimension, that entanglement at past infinity will be turned into temporary correlations, and thus temporary opportunities for interaction, during the bulk lifetime of the universe.

 

[dhillonv10]

So then studying the ds/CFT paper is probably a good idea, I think I will be doing that for the next few days. Originally I had in mind to go study twister theory and its implication that you provided but now in the light of these new developments, mitchell is it a good idea to spend time on twisters? The boundary-to-bulk mapping that is provided in that paper is derived from another paper so I'll probably start there and then come back to this one.

edit: i just finished reading your explanation of that email, and wow that's all i can say, in the beginning this idea was a mere speculation, but now i think this maybe taking a serious direction.

 

[qsa]

So then studying the ds/CFT paper is probably a good idea, I think I will be doing that for the next few days. Originally I had in mind to go study twister theory and its implication that you provided but now in the light of these new developments, mitchell is it a good idea to spend time on twisters? The boundary-to-bulk mapping that is provided in that paper is derived from another paper so I'll probably start there and then come back to this one.

I am not sure if this will help but this paper is FQXI contest paper that did not win but I like it because it is close to my idea.but my guess is that the use of time in modelling is the reason for all the problems, that is why it does not appear in mine naturally.

http://www.fqxi.org/community/forum/topic/950


I am somewhat disappointed in their winners, but I find Zenils paper is also good and he won third prize. also quantum graphity which I gather you like also won second prize.

http://www.fqxi.org/community/essay/winners/2011.1

 

[dhillonv10]

thanks for the links qsa, currently I've given up on the quantum graphity approach to this problem and I'm studying that ds/CFT paper. I'll look at the first paper more closely, that one appears to have something nice, atleast it addresses some of the things I'm interested in.

edit: that first paper actually describes precisely something i was speculating earlier, the reason why entanglement occurs instantaneously when the universe is supposed to follow a speed limit for light, but for all i know following VSL i could be wrong :)

 

[mitchell porter]

Herman Verlinde (Erik Verlinde's twin brother, also a physicist) gave a talk a few months ago called "Twistors and De Sitter Holography". No details are available, so it must be work in progress. (He coauthored another paper about twistors but it's not about dS/CFT.)

I can't say what order you should investigate these topics. They are all advanced, they are all connected, and they all depend on a lot of simpler ideas in mathematics and physics.

 

[dhillonv10]

I see, well since the dS/CFT paper is readily available, I'm going to start with that and the correlation functions. By the time I finish that, the twistors and de Sitter holography talk might be around.

 

[mitchell porter]

I meant to add another indication of how the development of dS/CFT lags the development of AdS/CFT.

In examples of AdS/CFT, we have a precise definition of the field theory on the boundary, and a precise or semi-precise definition of the gravity theory in the bulk. For example, consider the original example, d=4 N=4 Yang-Mills (which is the CFT in this example) dual to Type IIB superstring on AdS5 x S^5. I'll use http://arxiv.org/abs/hep-th/0201253" as a reference. On the boundary side, we know exactly what the fields are and how they interact (page 16). In the bulk, we at least have approximate equations of motion for the Type IIB string (page 29) and we can specify the space it is moving through (pages 43-45). And then we have a mapping between combinations of the boundary fields and states of the string - outline on page 49, some details on page 50.

In the first column on page 50, you will see many expressions of the form "tr ABC". A, B, C are fields from the boundary theory, ABC is their product, tr ABC is the http://en.wikipedia.org/wiki/Trace_%28linear_algebra%29" of the product. In the third column, you see fields from the bulk. (These are all actually vibrational or other modes of the superstrings in the bulk.) So the holographic correspondence is telling us that, for example, correlations between those bulk fields can actually be calculated from correlators of the corresponding boundary operators (the "tr ABC" products of boundary fields). None of this detail was visible from the beginning, by the way; Maldacena guessed the equivalence of the two theories, on the hypothesis that they are two ways of describing the same "black brane" in string theory, and then people painstakingly confirmed that the boundary operators in the first column have the right properties to match the bulk fields in the third column.

Now what do we have in dS/CFT? Basically, for all proposed examples of dS/CFT, we don't have the CFT - we can't list the boundary fields or say how they interact. (If anyone out there can prove me wrong, please do so.) It's as if, in the first column of the table on page 50, you just had "operator 1, operator 2,... operator 20", but you didn't have any of the "tr ABC" expressions providing the details. All people can do is specify the gross properties of the operators, especially the "conformal dimension", but they're just guessing that a CFT exists, in which there are field operator products with the necessary properties.

If this sounds like it might all be based on an illusion... Maldacena's original (1997) paper contained three examples of AdS/CFT duality. For the first case, he was able to say right away what the boundary theory was (it's N=4 YM, mentioned above). For the second case, it took ten years for the right theory to be found (in the "ABJM" paper - those are the initials of the authors). For the third case, he could specify the boundary theory but the theory in question lacks a tractable definition - people are working on this right now.

So while the lack of a fully realized concrete example of dS/CFT is a serious problem, it doesn't mean that it's an illusory idea, and in fact a lot of ideas and knowledge has been accumulated in the ten years since Andrew Strominger wrote the original dS/CFT paper. It's just that all of those ideas and all that knowledge is still preliminary; people are waiting for the breakthrough, and probably there has to be a conceptual breakthrough, some twist that no-one has thought of yet. For the second example of AdS/CFT in Maldacena's original paper, people were originally trying to employ a different Yang-Mills theory, but John Schwarz suggested that it might be a "Chern-Simons" theory, and eventually ABJM figured it out. For dS/CFT, David Lowe's technical idea for how to make it work, was to represent the geometric symmetries of the bulk differently in the CFT (using "principal series representations"), and also to modify ("deform") the CFT by a new parameter, q, and also to modify the bulk geometry in a way that he didn't quite specify... The last follow-up, to that "new twist" paper from 2003, seems to be 2006, so maybe the idea didn't work, or maybe it's in hibernation.

 

[dhillonv10]

Currently reading through the new twist paper, from a preliminary analysis these guys are aiming to reformulate the ds/CFT correspondence by replacing the classical isometry group with this new q version, and introduce the principal series representation. Also one interesting line I found was this:

Such a reformulation of dS/CFT is natural from the bulk point of view, since the quantization of a scalar field on ...

So that in some sense means that this new formulation of the theory, called qdS/CFT, may be what is needed to finish up

The real heart of the correspondence is the re-expression of the bulk correlation functions at past infinity, in terms of CFT operators.

The problem however is that even thought they state some parts of their new theory, they never explicitly mention how is it natural from the bulk's point of view. I think that part will be accomplished by expressing the bulk correlation functions in terms of CFT operators. I'll be finishing up this paper probably before the end of the coming week and in the meantime i'll post any other observations I make.

edit: please clarify this mitchell:

So the holographic correspondence is telling us that, for example, correlations between those bulk fields can actually be calculated from correlators of the corresponding boundary operators (the "tr ABC" products of boundary fields).

In that paper, here's the section that describes what you stated:

5.6 Mapping Type IIB Fields and CFT Operators
Given that we have established that the global symmetry groups on both sides of the
AdS/CFT correspondence coincide, it remains to show that the actual representations of
the supergroup SU(2, 2|4) also coincide on both sides.

So does that imply that there is to some extent a mapping established from bulk to the boundary in terms of AdS space?? If so couldn't that be extended out to dS spacetime using what you said earlier: (using the complex numbers approach)

So, returning to the paper: their region-on-the-boundary-to-point-in-the-bulk map for anti de Sitter space is an analytic continuation of the region-on-the-past-boundary-to-point-in-the-present-bulk map for de Sitter space. More precisely, they use a formula which makes sense in de Sitter space, because all the space and time distances in the formula are specified in real numbers, and then they transform that into a formula which looks like the anti de Sitter formula by making some quantities imaginary.

 

[mitchell porter]

So does that imply that there is to some extent a mapping established from bulk to the boundary in terms of AdS space?? If so couldn't that be extended out to dS spacetime using what you said earlier: (using the complex numbers approach)

I made a diagram for reference (see attachment)... I mentioned that you could analyse a holographic mapping, from bulk to boundary, into two stages. First, you go from the interior of the bulk to the edge of the bulk: for example, from a point in the interior to a region on the boundary. Then, you re-express everything in terms of the boundary theory, so that bulk fields become boundary operators.

The analytic continuation applies to the first stage, where you go from the interior to the edge. See my diagram. In AdS3/CFT2, you're going "sideways". The two-dimensional region on the boundary (black disk) has a space direction (around the cylinder) and a time direction (up the cylinder). But in dS3/CFT2, you just go back in time to past infinity, and the black disk is now entirely spacelike. Turning a space direction into a time direction, or the other way around, is where the complex numbers enter; it's called http://en.wikipedia.org/wiki/Wick_rotation" .

In both cases, what the diagram means is that you calculate something to do with the point at the tip of the cone, by summing over all the points in the black disk at the base of the cone. For example, you might be computing a two-point correlation function in the interior of the bulk. Each point would be the tip of a separate cone based on the boundary, and you would be re-expressing the bulk-to-bulk two-point correlation function as a double integral over correlation functions between every point in one black-disk region on the boundary and the other black-disk region on the boundary. And the analytic continuation means that you can express the integral for AdS space in terms of the integral for dS space with complex coordinate values, or vice versa.

OK, great. However, there are two problems. First, this is only the easy part of the true bulk-to-boundary mapping, we don't yet have the change of variables into the boundary CFT. Second, these cones are only localized structures; the global structure of AdS and dS space is different. It's similar to the difference between a Mobius strip and an ordinary untwisted rubber band. If you just look at one section, they look the same, but because of the twist, the Mobius strip can't fit into two dimensions in the way that an untwisted strip could. To globally transform the whole of a particular AdS/CFT correspondence into the whole of a particular dS/CFT correspondence, it would be as if the whole of the AdS boundary was covered in the black disks, and then you transformed the AdS boundary into the dS boundary.

In my diagram, the boundary of AdS3 is the outside of the cylinder, and the boundary of dS3 is supposed to be the surface of a sphere. It is actually possible to map a cylinder onto a sphere - if you make holes at two opposite points on a sphere and stretch them out into circles, and then straighten the sphere. So maybe some combination of this, with the analytic continuation into complex-valued coordinates, could be attempted, for a particular AdS/CFT pairing of theories. The question is, what do you end up with? Because for dS/CFT to work, you need to have much more than just a mapping between points in the bulk and points on the boundary. The field theory on the boundary has symmetries and they have to include the symmetries of the bulk theory. Or, to look at it another way, the boundary space has its own symmetries, and they have to be present in the bulk theory; in your quote, this is what "the supergroup SU(2,2|4)" refers to - the "superconformal" symmetries of the boundary theory.

Superconformal symmetry includes supersymmetry, and supersymmetry is always broken in de Sitter space, so that's already a problem. And in fact problems like these are part of the reason why David Lowe suggested a "qdS/CFT" using a different sort of symmetry representation; he's trying to invent something which is tailored to de Sitter space. So there are at least two possibilities. One is that there are AdS/CFT dualities that can be Wick-rotated to dS/CFT with the whole structure intact. (Maybe they would need to be completely non-supersymmetric AdS/CFT dualities, given that dS/CFT won't allow unbroken supersymmetry.) Another possibility is that dS/CFT is a separate thing from AdS/CFT, and that the algebraic details of AdS/CFT never cross over to dS/CFT.

Those are deep questions, but maybe I can say something to clarify what's happening in the original "analytic continuation to de Sitter space". In effect, they are saying "let's pretend that locally we are in de Sitter space, because the calculation is easier". When they integrate over a boundary region (black disk in the diagram), and perform analytic continuations, they are slipping back and forth between my AdS picture and my dS picture, but all they care about is the cone, they don't care about the global structure. So the fact that they can do this doesn't necessarily imply that that all the details of the second part of the correspondence (re-expressing the bulk correlation functions in terms of CFT operators) can also be swapped back and forth between the two pictures - the analytic continuation here only pertains to an intermediate step.

 

[dhillonv10]

thanks again for the clarification mitchell, so far you have presented a lot of information, and i want to make this post to collect the main ideas since its spread across 4 pages, then we can carry on the discussion. Please PM me if you want changes in this post, that way we can keep one post and I'll edit what changes are required.

Goal: Could a purely local interaction in a classical boundary field theory turn into a nonlocal interaction in its holographic image? Or more precisely stated: Re-expression of the bulk correlation functions at past infinity, in terms of CFT operators.

Approaches:

Explain quantum mechanics using the holographic principle by expressing both theories using Bohm's equations (Bohmian mechanics)

Grassmannian formalism: the discovery of a third framework, neither string theory (bulk) nor field theory (boundary), but something else outside space-time entirely, this is the framework where neither space-time locality nor quantum unitarity is "manifest", i.e. visible - you have to switch to the other perspectives to see them.

Map bulk nonlocality to boundary locality using twistors somehow. The "third theory" of Arkani-Hamed et al, which adds a third description to the bulk/boundary duality, is expressed in terms of twistors.


Papers:

Stochastic Quantization: http://arxiv.org/abs/0912.2105 in AdS/CFT

Entanglement spectrum and boundary theories with projected entangled-pair states: http://arxiv.org/abs/1103.3427

Chern-Simons Gauge Theory and the AdS(3)/CFT(2) Correspondence: http://arxiv.org/abs/hep-th/0403225

Entanglement Renormalization and Holography: http://arxiv.org/abs/0905.1317

A Duality For The S Matrix: http://arxiv.org/abs/0907.5418

Local bulk operators in AdS/CFT and the fate of the BTZ singularity: http://arxiv.org/abs/0710.4334

A new twist on dS/CFT: http://arxiv.org/abs/hep-th/0312282

A holographic view on physics out of equilibrium: http://arxiv.org/abs/1006.3675

 

[mitchell porter]

That covers most of it. I want to return to the topics of holographic noise and entropic gravity, too, eventually.

Meanwhile, I also realized (something I already knew), that the way you go from globally AdS to globally dS is by adding ingredients (branes, field fluxes) which will add enough positive curvature to outweigh the negative curvature of the AdS geometry. I mention an example in this new post on https://www.physicsforums.com/showthread.php?p=3353934".

 

[dhillonv10]

That was a very interesting post, now from http://docs.google.com/viewer?a=v&q...sig=AHIEtbTmz7irHqIdm1cAnD4vvaGI7uyuKQ&pli=1" presentation (slide 2) the bulk correlation functions have been written in terms of boundary operators in AdS (if I understand it correctly). Now we need to explore more on the AdS-to-dS uplift, I am going to look more into the papers mentioned in that post and see what I can find.

edit: This is basically the same thing you mentioned in #36, the idea of expressing bulk scalar field phi in terms of the boundary field phi_0. Now using the uplifting, we then maybe able to transform the AdS space to dS space and then we can have that scalar field in dS space.

edit 2: Just found another interesting paper: http://arxiv.org/abs/hep-th/0203208

They mention this on page 2:

Here we discuss a different proposal of extrapolating from AdS to dS spaces. We establish a duality between the two spaces which interchanges the role of coordinates and momenta for a scalar field. We thus show that a massive mode in dS space is dual to a tachyonic mode in AdS space.

and they are again using complex variables to accomplish a lot of this for instance the analytical continuation. The tacyonic nature however worries me in this case.

 

[mitchell porter]

This is basically the same thing you mentioned in #36, the idea of expressing bulk scalar field phi in terms of the boundary field phi_0. Now using the uplifting, we then maybe able to transform the AdS space to dS space and then we can have that scalar field in dS space.

Almost certainly counterparts of these formulas for de Sitter space do exist. However, the other part of holography is specifying the conformal field theory on the boundary, the fields of which are combined to create the "O" operators that are equivalent to the bulk fields close to the boundary. We now have many examples of AdS/CFT where the CFT is known, but we have no examples of dS/CFT where the CFT is known; and most of the examples of AdS-to-dS uplift that were constructed in string theory since 2004 start with an AdS model where the boundary CFT also isn't known. The 2009 paper by Polchinski and Silverstein, which I mention in the "dS/dS" post, was a first step towards finding AdS/CFT dual pairs which were also suitable for uplifting. So in those cases, at least the CFT is known on one side of the AdS-to-dS uplift - but only on one side.

Just found another interesting paper ... The tachyonic nature however worries me in this case.

A tachyonic mode of a field is now usually understood as an artefact of the field being in an unstable vacuum state. For example, see http://www.ift.uni.wroc.pl/~rdurka/index/Higgs.pdf" . If you start the field in a quantum state at the top of the Mexican hat potential, it will immediately move towards a lower-energy state in the valley below.

Particles in quantum field theory come about from quantum probability distributions over the Fourier modes we discussed earlier on. A quantum Fourier mode has an "occupation number" which is the number of particles with momentum corresponding to the wavelength of the mode (i.e. this is their de Broglie wavelength). A vacuum state is a quantum state for the field in which the occupation number is zero everywhere. Being at the top of the Mexican hat potential defines a vacuum state for the Higgs field in which excitations of the Fourier modes correspond to particles with negative mass squared. In terms of relativity, that would mean faster-than-light propagation, but here it means that the field is in an unstable state, and it decays to the stable lower energy state before any such tachyonic excitations could go anywhere. In the lower, more stable vacuum state, the Higgs particle now have positive mass squared.

So in contemporary physics, tachyons don't mean "faster than light", they mean "unstable vacuum". It's the same thing - particles with imaginary mass - but the second consequence turns out to be the relevant meaning. For example, you can see string theory papers about tachyon condensation between brane-antibrane configurations - all it means is that the brane configuration is unstable and will immediately annihilate into something else.

De Sitter vacua are usually and perhaps always unstable in string theory, so a fact about tachyonic modes in de Sitter space probably has to do with this instability, but the exact significance of this particular "duality" eludes me. The fact that it is an exchange between coordinate space and momentum space reminds me of the dual superconformal symmetry which exists in the most-studied examples of AdS/CFT. But there might be no connection; I'd have to study it properly to be sure.

 

[mitchell porter]

By the way, http://arxiv.org/abs/1102.2910" is Kabat, Lowe et al's latest on locality in the bulk - just a few months old! So even they won't be much further along than what you can read there.

In a sense, they're looking at the opposite topic to what's being discussed in this thread. Here we want to understand how locality on the boundary gets turned into nonlocality in the bulk. But what they are trying to do, is to see how to represent bulk locality on the boundary. That means two things - just being able to talk about a point in the bulk, and then, being able to talk about causal locality in the bulk (see what they say about commutation of spacelike operators - if they commute, that means there's no causal interaction at a distance). Everyone agrees that the bulk theory has to be nonlocal in some sense, but also that it ought to be approximately local - it's not an unanalyzable mess of nonlocal connectedness. So they are working in the language of the boundary CFT to describe bulk physics in a way that is as local as possible. But if they make any progress on that question, it should be relevant for us, because any left-over nonlocality that they can't eliminate must be a big clue to the exact nature of holographically induced nonlocality.

 

[sanoy19]

does quantum entaglement create all field that exist! as everything were bound together before big bang??

 

[marcus]

I started a separate thread for Sanoy's question:
https://www.physicsforums.com/showthread.php?t=507150

 

[dhillonv10]

I'm currently reading that paper and it is an impressive result that they are able to show how a massless scalar field in EAdS space is dual to massive scalars in dS space. But see that also brings up another concern I have, the scalar field phi that we have been discussing in various papers so far, those seem to be massless, I think. Now how'd things change if that scalar was to gain mass? If it doesn't change anything that we are already most of the way there to the mapping. We already have a well defined mapping from bulk to boundary in AdS in terms of a scalar field and now if there exists an uplift mechanism to dS then the mapping in AdS should hold as well. That last part, I need a bit of time to properly define it.

 

[mitchell porter]

I'm not sure which paper you're reading, and maybe I shouldn't distract you from this topic, but all of that is just about relating properties of a field in an AdS bulk to properties of a field in a dS bulk. The formulas for one field will be similar to formulas for the other field, except for a few alterations corresponding to the change from a negatively curved space to a positively curved space.

But all that is still just preliminary. The real AdS/CFT correspondence involves what I was talking about in #47: the re-expression of bulk fields near the boundary, in terms of a completely different set of fields on the boundary.

The fields of the boundary theory - call them A, B, C... - and combinations of them - dA/dx . B^2, or whatever - transform in a certain way under conformal transformations (re-scalings, mostly) of the boundary space. When you do this coordinate transformation on the boundary, the correlation functions, etc, have to be multipled by a quantity of the form z^n, where z expresses the magnitude of the re-scaling. For a given combination of boundary fields, the exponent n is called the "conformal dimension" of that combination. You can estimate n just from counting "tensor indices" (whether A, B are scalar, vector, how many space derivatives there are, etc), but then there's an extra "anomalous" contribution that comes from quantum mechanics. The full "anomalous conformal dimension" of a combination of field operators from the boundary theory then maps onto the mass of the corresponding field in the bulk. Also note, one field in the bulk corresponds to one combination of fields from the boundary. The capital-O operators which show up in these papers by David Lowe refer to unspecified combinations of fields from the unspecified boundary CFT (the "trace ABC" expressions I mentioned in comment #47).

This is the algebraic complexity which is at the heart of AdS/CFT (or at least, it was the first really difficult aspect of the correspondence to be investigated and confirmed, since it's quite hard to calculate these anomalous dimensions). It starts out as an algebraic relation between combinations of boundary field operators, and bulk fields near the boundary. Once you have that, it's a much simpler thing to extend the relation so it also applies to bulk fields away from the boundary - that just corresponds to higher energy scales on the boundary, or (same thing) to summing over increasingly large regions on the boundary, as in these papers by Lowe.

But so far as I can see, no-one has any real understanding of what happens to this algebraic relation when you go from AdS to dS. How could they, when they don't have any full examples of dS/CFT to work with, just guesses? We don't know if the AdS/CFT algebraic relation survives but gets changed, or if it is completely destroyed and a completely different one takes its place. So, this is a hard problem, even before you start trying to derive quantum mechanics itself from holography. :-)

 

[Finbar]

Isn't there a Euclidean-Euclidean version of AdS/CFT? In which case the boundary should have a Bohmian interpretation, shouldn't it?

But of course this wouldn't be a derivation of QM, since it the Bohmian interpretation is QM.

atyy,

I wonder what your getting at here? can you elaborate a little. I find it interesting that Bohm had a "holographic" interpretation of QM.

http://en.wikipedia.org/wiki/Implicate_and_explicate_order_according_to_David_Bohm


These ideas come at least 14 years or so before the "holographic principle" for QG was first put forward!


Of coarse its not clear whether the two ideas of holographic are directly related. But it would seem likely to me.

 

[dhillonv10]

thanks for the reply mitchell, in that last post I was referring to: An AdS/dS duality for a scalar particle. I do understand to some extent that reading that paper won't provide the full correspondence that we need, the ideas presented there seemed interesting though. But it is as you say, this problem is indeed very difficult and part of the reason is the lack of fully worked examples, in that case I think we may simply have to use indirect methods or guesses :) first of which is the wick rotation, http://arxiv.org/abs/0710.4334" paper explores some of that. Now I found another very interesting indirect method that is a little more than half-way developed:

Conformal anomaly from dS/CFT correspondence:

Abstract:
In frames of dS/CFT correspondence suggested by Strominger we cal-
culate holographic conformal anomaly for dual euclidean CFT. The holo-
graphic renormalization group method is used for this purpose. It is ex-
plicitly demonstrated that two-dimensional and four-dimensional conformal
anomalies (or corresponding central charges) have the same form as those
obtained in AdS/CFT duality.

And in the conclusion they mention this:

We should note that holographic conformal anomaly obtained from
dS/CFT duality seems to be identical with that from AdS/CFT one. This
shows that obtained central charge from dS/CFT duality itself is the same
with that from AdS/CFT. Nevertheless, it does not mean that boundary
CFTs should be necessarily the same because there may exist several differ-
ent theories with the same central charge. Finally, let us note that the fact
that holographic conformal anomaly from AdS/CFT or dS/CFT duality is
the same suggests that both these dualities are the consequence of some un-
derlying fundamental principle. Even more, one can speculate on existence
of more dualities of such sort, also for other spaces.

Even though we are not looking for conformal anomalies, this gives some evidence that there is an indirect method that can be applied to uplift the AdS space to dS.

 

[mitchell porter]

I haven't decoded all of that yet. But it's interesting to see that http://arxiv.org/abs/hep-th/9912012" (computing the conformal anomaly using holographic RG flow) employs the Hamilton-Jacobi equations, because they also offer a path to the Bohmian approach to quantum mechanics. You may have seen news stories recently about the reconstruction of definite trajectories for photons in a double-slit experiment, using "weak-valued measurements"; those were "Bohmian trajectories". So, here we're close to something very basic about how quantum mechanics works.

 

[dhillonv10]

Just an update, I've been working on a related problem in the meantime however, today two very interesting papers came up, I am not sure if anyone mentioned those already or not.

1. dS/CFT Duality on the Brane with a Topological Twist: A C Petkou, G Siopsis (2001)

Abstract:

We consider a brane universe in an asymptotically de Sitter background spacetime of arbitrary dimensionality. In particular, the bulk spacetime is described by a ``topological de Sitter'' solution, which has recently been investigated by Cai, Myung and Zhang. In the current study, we begin by showing that the brane evolution is described by Friedmann-like equations for radiative matter. Next, on the basis of the dS/CFT correspondence, we identify the thermodynamic properties of the brane universe. We then demonstrate that many (if not all) of the holographic aspects of analogous AdS-bulk scenarios persist. These include a (generalized) Cardy-Verlinde form for the CFT entropy and various coincidences when the brane crosses the cosmological horizon.

This in some sense goes back to the idea bf being able to uplift AdS to dS and that may preserve some of the holographic dualities.

2. dS/CFT Correspondence in Two Dimensions: Scott Ness, George Siopsis (2002)

Abstract:

We discuss the quantization of a scalar particle moving in two-dimensional de Sitter space. We construct the conformal quantum mechanical model on the asymptotic boundary of de Sitter space in the infinite past. We obtain explicit expressions for the generators of the conformal group and calculate the eigenvalues of the Hamiltonian. We also show that two-point correlators are in agreement with the Green function one obtains from the wave equation in the bulk de Sitter space.

Restricted dimensionality however, if I understand this correctly, it has something to do with the wave function from the quantum mechanical model constructed at the boundary to the correlators in bulk.

 

[mitchell porter]

I finally got to see one of the http://pirsa.org/11060046/".

But the sense in which it's a holographic construction eludes me. Holography is mentioned in the first ten minutes, and then again in the very last minute. There are mappings, q and q_T (q transpose, the inverse of q), which are not bulk-to-boundary mappings but bulk-to-"screen" mappings, where a screen is a surface in the bulk of one less dimension. There is a remark at 34 minutes that space-time points become the lowest Landau level of something in one extra dimension. At 45 minutes the matrices q and q_T show up again, as noncommutative space-time coordinates for strings stretching between a stack of N D4-branes and a cloud of k D0-branes. Then all this gets uplifted to a six-dimensional space of the form S^4 x S^2 - the D4-brane become space-filling D6-branes and the D0-branes become D2-branes wrapping the S^2 - and this six-dimensional space happens to be twistor space! - 4-dimensional space with an extra "sphere" at each point, corresponding to directions in 3-dimensional space. Again, the strings between these branes implement a version of twistor string theory, with one part being equivalent to the self-dual part of N=4 Yang-Mills, and another part giving you the rest of N=4 Yang-Mills coupled to conformal supergravity. Verlinde (http://arxiv.org/abs/1104.2605" , because the classical continuum picture no longer applies at very short distances), and he says it's holographic too - but that's the part I don't understand - at the end he says there's a projection onto the "twistor line", but I thought that was equivalent to one of the "S^2"s, so if he's talking about the reduction from 6d perspective to 4d perspective, it just seems like Kaluza-Klein - approximating in a way that neglects the compact extra dimensions - and not the dramatic holographic elimination of one large dimension.

So I don't get it, but it's extremely interesting, and will hopefully make more sense to me in the near future.

 

[dhillonv10]

Thanks for the link to the talk, I was looking around for the talk on Simulating the universe as a quantum computer when i found the talks from the Holographic Cosmology 2.0. There was some talk on the Denef paper as well. Anyways the idea of using a screen is very interesting, it reminds me of the Grassimian representation that we talked about before, the fact that you would use a third theory that is more fundamental. You make the bulk dual to the screen and then the screen to the boundary, so the paper I mentioned before: dS/CFT Correspondence in Two Dimensions: Scott Ness, George Siopsis (2002) might actually work. I'll comment again with questions and such as I watch the talk.

update: There is also a talk on uplifting, titled: Uplifting AdS/CFT to Cosmology

 

[Fyzix]

I ressurrect this thread.

Could you outline your main thoughts in layman terms?
What is it you are thinking is going on in the horizon that gives us the illusion of randomness and nonlocality?

 

[dhillonv10]

Fyzix: this thread isn't dead yet, we are simply waiting, at Strings 2011, Herman et. al announced that they had worked out a complete example of dS/CFT and the paper will be out later this month. Once that's in, then we can do a lot more instead of making guesses as to what really happens because of the lack of an example.