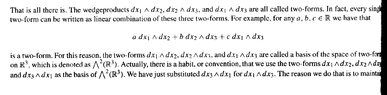The Space of 2-Forms .... Fortney, Darling and Weintraub ....

[Math Amateur]

I have a question regarding the nature of 2-forms (indeed k-forms ... but I'll focus the question on two forms ... ) ... Defining 2-forms and the space $$ {\bigwedge}^2 ( \mathbb{R}^3 )$$ , Jon Fortney in his book: A Visual Introduction to Differential Forms and Calculus on Manifolds, writes the following:View attachment 8783R. W. R. Darling in his book defines $$ { \bigwedge}^2 V $$ similarly when he writes the following:View attachment 8784... BUT ...Steven Weintraub in his book: Differential Forms: Theory and Practice defines k-forms (and hence 2-forms ...) as follows:View attachment 8785(NOTE: Weintraub omits the wedge notation writing the wedge product $$dx \wedge dy$$ as just $$dx dy$$ ... ... )
My question is ... how do we reconcile the differences between Fortney and Darling's definition of a 2-form and the space of two forms ... with Weintraub's definition ...

Essentially ... Fortney defines a 2-form as

$$a dx_1 \wedge dx_2 + b dx_2 \wedge dx_3 + c dx_1 \wedge dx_3 $$

where $$a,b, c \in \mathbb{R} $$... while Weintraub defines a 2-form as $$f_1 dx_1 \wedge dx_2 + f_2 dx_2 \wedge dx_3 + f_3 dx_1 \wedge dx_3 $$

where $$f_1, f_2,$$ and $$f_3$$ are smooth functions ...
Can someone please help reconcile the differences between the definitions of Fortney and Weintraub ...?Help will be appreciated ...

Peter
EDIT ... reflection ... the definitions could be very similar ( ... the same ...? ... ) since the smooth functions are (I think) real-valued functions ... and so when evaluated at a point are real numbers ... does that make sense of the above?Peter

 

[GJA]

Hi Peter,

Weintraub is defining a differential $k$-form, which is one where the smooth function $f$ is used to allow the coefficients to vary from point to point (as opposed to the fixed values of $a$, $b$, and $c$ used by Fortney). Also, you are correct that $f$ is a smooth, real-valued function.

 

[Math Amateur]

Hi Peter,

Weintraub is defining a differential $k$-form, which is one where the smooth function $f$ is used to allow the coefficients to vary from point to point (as opposed to the fixed values of $a$, $b$, and $c$ used by Fortney). Also, you are correct that $f$ is a smooth, real-valued function.

Thanks for the help, GJA ...

Peter