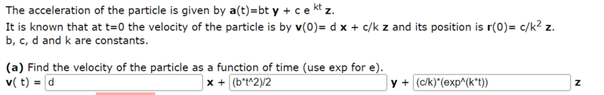SUMMARY
The discussion focuses on determining the velocity of a particle as a function of time, given the acceleration equation a(t) = bt y + c e^(kt) z. The initial conditions specify that at t=0, the velocity is v(0) = d x + (c/k) z and the position is r(0) = (c/k^2) z. A participant questions the correct form of the velocity equation, suggesting it should be (c/k) * exp(kt) without the exponent notation. The relevant equation for velocity is v(t) = ∫ a(t) dt.
PREREQUISITES
- Understanding of calculus, specifically integration techniques.
- Familiarity with vector notation in physics.
- Knowledge of exponential functions and their properties.
- Basic concepts of particle motion and kinematics.
NEXT STEPS
- Study integration techniques for solving differential equations.
- Explore the properties of exponential functions in physics applications.
- Review vector calculus and its application in motion equations.
- Investigate the implications of initial conditions on particle motion.
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and motion equations, as well as educators looking for examples of particle velocity derivation.