Sunny007
- 2
- 0
Suppose a square shaped object has an initial length of L1 and final length (after thermal expansion) of L2. Initial temperature is T1 and final temperature is T2. Suppose it has an area of A. So initial area is A1 and final area is A2 (after thermal expansion). Here A1 = (L1)^2 and A2 = (L2)^2 . Now area expansion coefficient B(beta) = (A2-A1)/A1*(T2-T1). or, B = (L2^2 - L1^2)/ L1*L1*(T2-T1) or, B = (L2-L1)(L2+L1)/ L1*L1*(T2-T1) or B = (L2-L1)*a/ L1 [ suppose alpha = a and we know that alpha = (L2-L1)/L1(T2-T1) ] or, 2a = (L2-L1)*a/ L1 or 2 = (L2-L1)/ L1 [ cancelling alpha from both sides) or, 2L1 = L2-L1 or L1= L2. So now does that mean that it has no expansion as Final length and initial length is equal?
Here is an image of the calculation.
[Mentor Note -- Image rotated to fix sideways orientation]
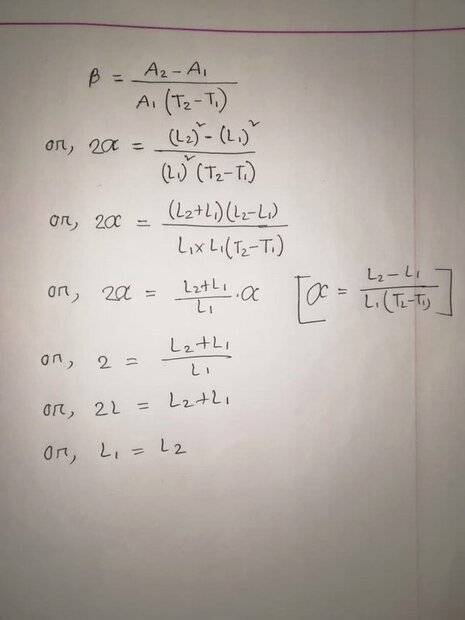


Here is an image of the calculation.
[Mentor Note -- Image rotated to fix sideways orientation]

Last edited by a moderator: