JoelKTH
- 29
- 1
- Homework Statement
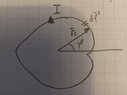
- A thin wire that carries the current I is bent in a heart-shaped curve according to the equation r_c=r_0 e^k|phi| for |phi|<= pi, where r_c is the distance from origo to a point on the curve. Calculate the magnetic flow B in origo.
- Relevant Equations
- Biot Savarts Law
Hi,
So I know I am to use Biot Savarts law dB= (my_0/4pi)* (I dl x (r-r')/|r-r'|^3 where r=0 because its in origo and r'=r'_c(r'_hat).
This makes (r-r')= -r'_c(r'_hat) and |r-r'|^3= r_c^3.
From previous questions, I have defined dl' as the infinitesimal displacement of r'(phi) when phi' is increasing with dphi along the curve.
Usually its dl'/dphi = r_hat --> dl= r_hat dphi and then I use Biot Savarts law. However I get wrong result here.
My professor tells me to use dl=r_c' dphi' phi_hat + dr'_c r_hat_c.
Why is this intuitively correct? I am having some problem wrapping my head around this. How can I derive it from the dl' expression? Or know if there are any other shapes that do not only depend on phi.
//
So I know I am to use Biot Savarts law dB= (my_0/4pi)* (I dl x (r-r')/|r-r'|^3 where r=0 because its in origo and r'=r'_c(r'_hat).
This makes (r-r')= -r'_c(r'_hat) and |r-r'|^3= r_c^3.
From previous questions, I have defined dl' as the infinitesimal displacement of r'(phi) when phi' is increasing with dphi along the curve.
Usually its dl'/dphi = r_hat --> dl= r_hat dphi and then I use Biot Savarts law. However I get wrong result here.
My professor tells me to use dl=r_c' dphi' phi_hat + dr'_c r_hat_c.
Why is this intuitively correct? I am having some problem wrapping my head around this. How can I derive it from the dl' expression? Or know if there are any other shapes that do not only depend on phi.
//