MermaidWonders
- 112
- 0
How many isomers are there with the following description?
- Thioesters with the formula ${C}_{4}{H}_{8}OS$?
I was able to draw 2 of them, but apparently, the answer key showed and stated that there are 4. I am confused about why the following two are possibliities:
View attachment 8117
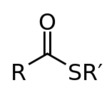
I thought that thioesters are the functional groups where a C double-bonded to O is attached to both an R group and S, with S itself being attached to an R group. So, I was wondering how the 2 structures in the above attachment could be thioesters when the C that is double-bonded to O isn't attached to an R group but is instead to an H?
- Thioesters with the formula ${C}_{4}{H}_{8}OS$?
I was able to draw 2 of them, but apparently, the answer key showed and stated that there are 4. I am confused about why the following two are possibliities:
View attachment 8117
I thought that thioesters are the functional groups where a C double-bonded to O is attached to both an R group and S, with S itself being attached to an R group. So, I was wondering how the 2 structures in the above attachment could be thioesters when the C that is double-bonded to O isn't attached to an R group but is instead to an H?