aerohead_18
- 33
- 4
This isn't for any particular project or assignment, but I've tried solving this in the past and haven't figured it out. Say you have an RC seaplane, like the one pictured, with the engine mounted well above and aft the CG. You're going to need to angle it down a little to counteract the pitch-down moment produced by the thrust acting above the CG.

Here's what I have so far.
Let's say the motor is 16" behind the CG and 4" above it, and it's generating 5lbs of thrust. To balance the moments, you would set it up like:
(TsinA)y=(TcosA)x
where T=thrust, A=motor angle from x-axis, y=position behind the CG, and x=position above the CG. Plugging in the values:
(5sinA)16=(5cosA)4
...which reduces to:
4sinA=cosA
As far as I know there isn't any way to solve that algebraically. The only way I could think of to solve for A might be graphing the functions f(x)=4sinA and g(x)=cosA and maybe use one of the solutions to find the angle where the two thrust components are equal. Below are the two functions graphed and some of their solutions.
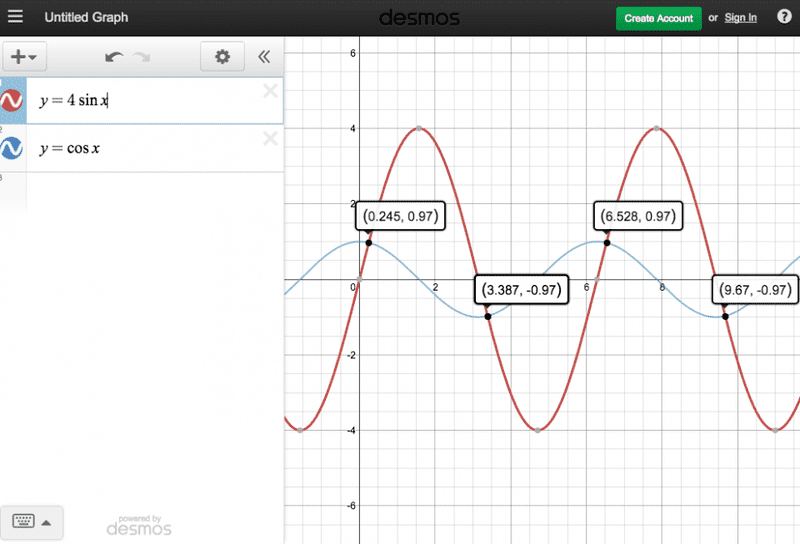
So, assuming I'm on the right track, where do I go from here? I initially thought the x-value of each solution would be a possible motor angle, but if you plug that back into the equation above the two sides aren't equal. So how on Earth would I do this?
Here's what I have so far.
Let's say the motor is 16" behind the CG and 4" above it, and it's generating 5lbs of thrust. To balance the moments, you would set it up like:
(TsinA)y=(TcosA)x
where T=thrust, A=motor angle from x-axis, y=position behind the CG, and x=position above the CG. Plugging in the values:
(5sinA)16=(5cosA)4
...which reduces to:
4sinA=cosA
As far as I know there isn't any way to solve that algebraically. The only way I could think of to solve for A might be graphing the functions f(x)=4sinA and g(x)=cosA and maybe use one of the solutions to find the angle where the two thrust components are equal. Below are the two functions graphed and some of their solutions.
So, assuming I'm on the right track, where do I go from here? I initially thought the x-value of each solution would be a possible motor angle, but if you plug that back into the equation above the two sides aren't equal. So how on Earth would I do this?