What is the connection between long, narrow bodies of water and harmonic waves?

[DaveC426913]

Full disclosure: it's not tidal; I'm pretty sure it's a longitudinal harmonic wave - but I don't know the terminology.

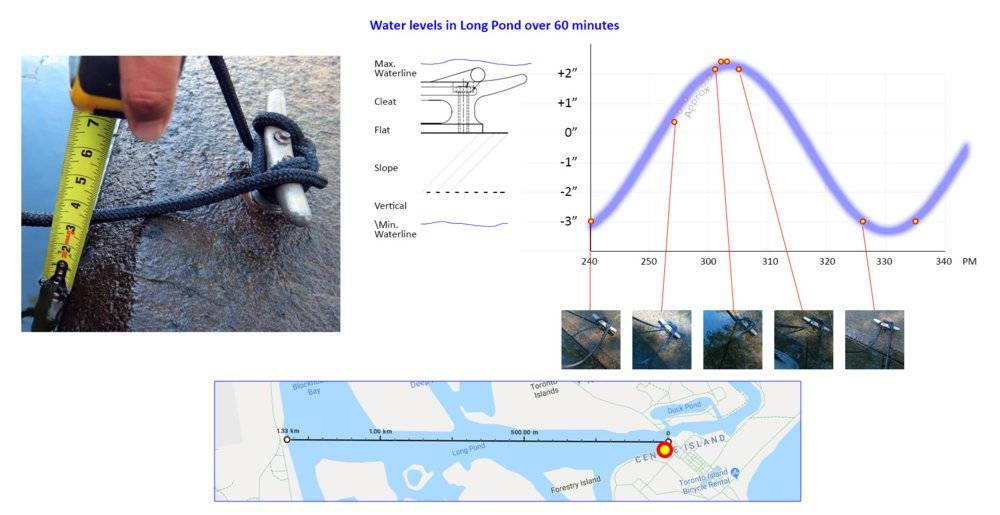
So today my bro and I went for a sail to Centre Island in Lake Ontario, as we often do. Lake Ontario is currently at its highest level in a long time - certainly in my lifetime. We go to Long Pond - an area of the islands that is 1.33km long and 100m wide and about 20ft depth - it's often used from dragon boat racing.

Where we usually pull up to the wall is currently awash. When we stepped out to tie off, we were standing in two inches of water - the tie-off cleats were submerged. We grabbed some food at the village to eat on the boat.

When we got back to the boat, we were standing on dry land. The water level had dropped by 5 inches. So I took a pic. A half hour later the wall was once again submerged. I watched it carefully, taking pictures every few minutes, and indeed the water level crept back down again.

At first I assumed it was wind surge - assuming the wind was changing direction and pushing the water up then down at this end of the pond, but since the wind was very light and didn't really change direction, yet the water level rose and fell with regularity, I've since concluded that this is a harmonic wave running back and forth along the pond.

I've read about this before - very long, very narrow lakes have this phenomenon - Lake Champlain has one, Loch Ness has one.

I'm now curious if there is a correlation between the dimensions of the body of water and its harmonic wave.

I made a thing:

 

[TeethWhitener]

It’s called a seiche. More info:
https://en.m.wikipedia.org/wiki/Seiche#Lake_seiches

 

[DaveC426913]

Thank you!

 

[DaveC426913]

Hm. I'm getting very unexpected results from the formula.

$$T=\frac{2L}{\sqrt{gh}}$$

L = length = 1.33km = 1333m
h = depth = 6m
g = gravitational acc = 9.8m/s^2

$T~=~2L/\sqrt{gh}$
$~=~2(1333)/\sqrt{9.8(6)}$
$~=~348s$

That's only 5m48s.
I'm observing ~60mins.

 

[jrmichler]

That equation is an approximation that assumes a rectangular lake. There is a good discussion of seiches in Limnology, by Robert G. Wetzel.

We measured several seiche frequencies in Trout Lake, located in Vilas County, Wisconsin, USA. None of those frequencies were close to the frequency from that equation. But that lake is not even close to rectangular. The measurements were at the south end of the lake and taken last summer.

 

[DaveC426913]

None of those frequencies were close to the frequency from that equation. But that lake is not even close to rectangular.

Thanks. Although my prediction is off by an order of magnitude.

Granted, my estimate of average depth is very generous - 6m is surely only at the centre - but even if I halve that to 3m, that only lengthens the period to 491s or 8m11s.

Other possibilities, though still a lousy fit:
Toronto Inner Harbour: 3.3km x 22m = 449s = 7m29s.
Lake Ontario: 310km x 86m = 10,678s = 178m = 2h58m.

 

[TeethWhitener]

The Wikipedia page for Lake Ontario states (without citation) that the lake has a naturally occurring seiche of 11 minutes. But NOAA:
https://oceanservice.noaa.gov/facts/seiche.html
claims that seiches in the Great Lakes can have a period of between 4 and 7 hours, and are often mistaken for tides.

Edit: also, in post #6, you forgot to multiply by two in the Lake Ontario calculation, so the fundamental resonance period is around 6 hours instead of 3. This level of agreement with NOAA is good, because Lake Ontario is pretty darn rectangular, as lakes go.

 

[OmCheeto]

Thanks. Although my prediction is off by an order of magnitude.

Granted, my estimate of average depth is very generous - 6m is surely only at the centre - but even if I halve that to 3m, that only lengthens the period to 491s or 8m11s.

Other possibilities, though still a lousy fit:
Toronto Inner Harbour: 3.3km x 22m = 449s = 7m29s.
Lake Ontario: 310km x 86m = 10,678s = 178m = 2h58m.

If I plug in the number for the width of Lake Ontario, measured from Toronto Island: 45,000 meters
I get a predicted period of 52 minutes.
Almost a bullseye to your measured 54 minutes.

T = 2 * L / √(g * h)
2 * 45,000 meters / √(9.8 m/s^2 * 86 m) = 3100 sec = 52 minutes

I checked the depths from Toronto Island to the Welland Canal, and 86 m is probably still a fairly good number.
[ref: NOAA chart]

Btw, when I solved for the depth of the Long Pond using your original numbers, I got a depth of 7 cm.
depth = (2 * L / T)^2 / g
depth = (2 * 1330 m / 3220 seconds)^2 / g = 0.07 meters = 7 cm

A tad shallow for your sailboat.

 

[DaveC426913]

If I plug in the number for the width of Lake Ontario, measured from Toronto Island: 45,000 meters
I get a predicted period of 52 minutes.
Almost a bullseye to your measured 54 minutes.

T = 2 * L / √(g * h)
2 * 45,000 meters / √(9.8 m/s^2 * 86 m) = 3100 sec = 52 minutes

Very cool. Today I was trying to reverse engineer the formula: what length/depth body of water would produce the results I saw? It seemed a pointless exercise though because it never occurred to me that seiches would work across the short dimension of a body.

But you know what? This makes perfect sense. Sunday was unusual in that it was a Northerly wind across the lake (it's usually Westerly).

Thanks! That is highly plausible!

depth = (2 * 1330 m / 3220 seconds)^2 / g = 0.07 meters = 7 cm

A tad shallow for your sailboat.

But only a tad... :)

 

[davenn]

It’s called a seiche. More info:
https://en.m.wikipedia.org/wiki/Seiche#Lake_seiches

Lake seichesEdit

Low rhythmic seiches are almost always present on larger lakes. They are usually unnoticeable among the common wave patterns, except during periods of unusual calm. Harbours, https://en.m.wikipedia.org/wiki/Headlands_and_bays, and estuaries are often prone to small seiches with amplitudes of a few centimetres and periods of a few minutes.

Among other lakes well known for their regular seiches is New Zealand's Lake Wakatipu, which varies its surface height at Queenstown by 20 centimetres in a 27-minute cycle.

Well we live and learn. I am well familiar with this example being that L. Wakatipu was in my homeland
back yard. But I never knew, till now, that it was the production of a seiche.

Thanks for that link, @TeethWhitener

Dave

 

[alva3]

Can some seiches be (technically) considered longitudinal waves?

 

[BillTre]

One of the greatest fossil finds ever has been partially attributed to the effect of seiches.
The seiches are though to have been caused by earthquakes from the Yucatan impact preceding the dinosaur extinction.
Its thought that the waves stirred up the water so much that it made a slurry of animals, animal parts, mud, and debris. This was then layered over by microtekties, and dust and ash from the impact.
Here is a PF thread on it.