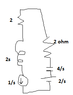
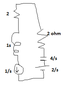
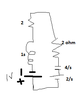
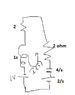
Converting to laplace I get
The L becomes 1s. The C becomes 4/s
The resistances are in series so that becomes 4 ohm.
For t < 0 the current through inductor is 1A as it is short circuit.
The voltage across Capacitor is 2V
So now when switch is open
the inductor will be 1A current source and the capacitor will be 2V voltage source.
Voltage across capacitor is Ldi/dt + 4(current) = 1di/dt + 4i = 2V(c)
Using laplace I get
Now using kvl I get
2/s = (1/s) (4/s + 4 + 1s)
So 2 = 4/s + 4 + 1s
so 0 = 4/s + 2 + s
s
2 + 2s + 4 = 0
Now how to proceed?
Book answer is 0.5
I'll do guess work
Laplace is V(s) = [ s^2 + 2s + 4 ] I(s)
So we do inverse laplace
I(s) = V(s) / (s^2 + 2s + 4)
Which is I(t) = V(t) e^[-(1+j1.732)t]
And time constant is when the e(raised to part) becomes e raised to 1
So (1 + j1.732)t = 1
t = inverse and inverse of this is 0.5
But I got this only cause answer was given. It's like I went backwards.
Laplace is V(s) = [ s^2 + 2s + 4 ] I(s)
I didn't understand after this.
Why not do laplace inverse now?