Time of closest approach between two particles

Click For Summary
SUMMARY

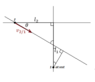
The forum discussion centers on calculating the time of closest approach between two particles moving at constant speeds, ##v_1## and ##v_2##, along mutually perpendicular lines, starting from distances ##l_1## and ##l_2## from the intersection point. The participants explore using Galilean transformations and relative velocity concepts to derive the minimum distance formula, expressed as ##min=d* \frac{v_2}{\sqrt{v_1^{2}+v_2^{2}}}##. The discussion emphasizes the importance of correctly interpreting the velocity vectors and initial positions to establish the geometric relationships necessary for solving the problem.

PREREQUISITES
  • Understanding of Galilean transformations in classical mechanics.
  • Knowledge of vector representation of motion and relative velocity.
  • Familiarity with trigonometric relationships in right triangles.
  • Ability to analyze motion in two dimensions with respect to a reference frame.
NEXT STEPS
  • Study the application of Galilean transformations in different reference frames.
  • Learn how to derive minimum distances using geometric constructions in physics.
  • Explore the concept of angular momentum conservation in two-dimensional motion.
  • Investigate the mathematical formulation of relative velocity in particle dynamics.
USEFUL FOR

Students and educators in physics, particularly those focusing on classical mechanics, as well as anyone interested in solving problems related to motion and distance calculations in two-dimensional systems.

  • #31
TSny said:
Yes. But you are only looking for the minimum distance between them. In the figure on the right in post #23, can you draw the line of motion of 2 in this frame of reference? Can you identify the point on the line of motion that corresponds to the minimum distance between them?
It would be a line that goes through the velocity vector. I think that the point that would corresponds to the minimum distance would be when the point 1 and the line of motion of 2 make a prepedicular line, right?
 
Physics news on Phys.org
  • #32
Davidllerenav said:
It would be a line that goes through the velocity vector. I think that the pint that would correspond to the minimum distnace would be when the point 1 and line of motion of 2 make a prepedicular line, right?
Yes, if I'm interpreting what you said correctly.
 
  • #33
TSny said:
Yes, if I'm interpreting what you said correctly.
Ok. so I have to make a triangle, right? But what would be the sides? One would be unknown since it is the minimum distance. What about the other two? I think that one would be the distance at time ##t=0## and the other the line of motion of 2.
 
Last edited:
  • #34
Davidllerenav said:
Ok. so I have to make a triangle, right? But what would be the sides? One would be unknown since it is the minimum distance. What about the other two? I think that one would be the distance at time ##t=0## and the other the line of motion of 2.
I don't believe that the line segment representing the initial distance between the objects will be of use. If you've drawn the trajectory of 2 and the line segment representing dmin, you might see two right triangles that you can work with.
 
  • #35
Davidllerenav said:
when the point 1 and the line of motion of 2 make a prepedicular line
show us in the drawing ...
 
  • #36
Davidllerenav said:
Ok. so I have to make a triangle, right? To find the minimum distance.
TSny said:
I don't believe that the line segment representing the initial distance between the objects will be of use. If you've drawn the trajectory of 2 and the line segment representing dmin, you might see two right triangles that you can work with.
BvU said:
show us in the drawing ...
Like this?
 

Attachments

  • 5.png
    5.png
    1.8 KB · Views: 399
  • Like
Likes   Reactions: BvU
  • #37
Davidllerenav said:
Like this?
Yes. You can work with the two right triangles in the diagram to find dmin.

There are other geometrical constructions that can be used to get the answer, including constructions that do make use of the line between the two initial positions of the objects. So, you should explore various approaches.
 
  • #38
TSny said:
Yes. You can work with the two right triangles in the diagram to find dmin.

There are other geometrical constructions that can be used to get the answer, including constructions that do make use of the line between the two initial positions of the objects. So, you should explore various approaches.
Thanks, I will look for other ways.
 
  • #39
Davidllerenav said:
Thanks, I will look for other ways.
You might also wish to consider that in the reference frame where object 1 is at rest at the origin, the angular momentum of 2 about the origin is conserved. This means that the initial angular momentum is the same as the angular momentum at the point of closest approach.
 
  • #40
kuruman said:
You might also wish to consider that in the reference frame where object 1 is at rest at the origin, the angular momentum of 2 about the origin is conserved. This means that the initial angular momentum is the same as the angular momentum at the point of closest approach.
I haven't seen momentum in my class yet.
 
  • #41
You don't really need it but it's a compact way to express what diagram to draw. It involves making use of the line between the two initial positions of the objects as @TSny suggested in #37.
 
  • #42
What is galilean transformation? I was able to do this problem easily using maxisimation of a function using differentiation. It's from I.E. Irodov.
 
  • #43
PhysicsKT said:
What is galilean transformation? I was able to do this problem easily using maxisimation of a function using differentiation. It's from I.E. Irodov.
It's what your friend says it is.
google is your friend :rolleyes: -- at least in some cases.
 

Similar threads

Collision between two uniformly moving particles
  • · Replies 7 ·
Replies
7
Views
2K
The speed of the point of intersection of two uniformly moving lines
  • · Replies 24 ·
Replies
24
Views
2K
Closest distance of approach between 2 charged particles
  • · Replies 5 ·
Replies
5
Views
1K
Doppler effect in Special relativity -- Solution verification
  • · Replies 1 ·
Replies
1
Views
1K
Should I use time dilation or length contraction?
  • · Replies 5 ·
Replies
5
Views
3K
Closest approach of alpha particle - two separate methods
  • · Replies 4 ·
Replies
4
Views
1K
What is the intersection point of two objects on a position vs time graph?
  • · Replies 10 ·
Replies
10
Views
2K
Velocity of a particle with some condition
  • · Replies 22 ·
Replies
22
Views
4K
Charged particle in Electric and Magnetic field
  • · Replies 33 ·
2
Replies
33
Views
3K
Horizontal impulse on a ball at rest on a plane (with friction)
  • · Replies 14 ·
Replies
14
Views
3K