- #1
SilverSoldier
- 26
- 3
- Homework Statement
- A uniform rectangular rod of length ##L##, having mass ##M## is placed at the edge of a frictionless table so that some portion of the rod rests on the table, and the other portion extends out of the table, and its center of gravity ##G## is a distance ##x## away from the edge of the table.
A block of mass ##m## is initially placed at the far end of the part of rod resting on the table, and given a velocity ##v##. If the coefficient of kinetic friction between the rod and the object is ##mu##, what must be the minimum value of ##v##, so that the rod can be made to topple over the table?
- Relevant Equations
- Equations of motion
Kinetic friction = ##\mu_k\cdot N##
Momentum = ##mv##
Torque = ##F\times d##
Here is a diagram of the situation.
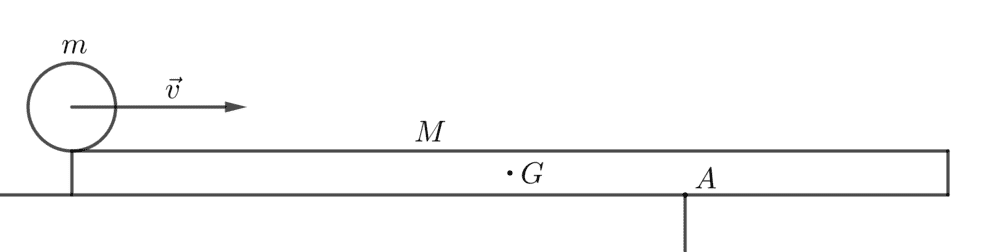I first marked the forces acting on the system.
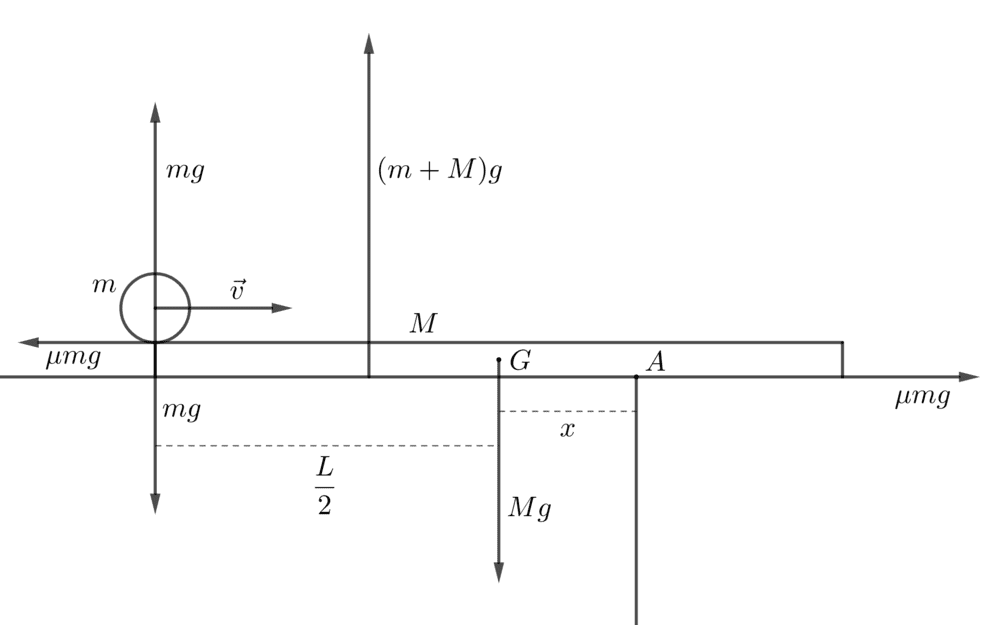I understand that for this rod to topple over, there must be a net moment about point ##A##. But how exactly should I approach this problem?
Isn't it so, that irrespective of the velocity given to the block, at some point both the rod and block will acquire equal velocities as a result of their acceleration and deceleration, and then just continue moving forward at that velocity?
If by any chance that were not the case, I tried solving it as follows.
First I calculate the distance to the center of gravity, say ##G'##, of the system from ##A##. We have
$$
GG'=\dfrac{m}{m+M}\cdot\dfrac{L}{2},
$$
and so we have
$$
\begin{align*}
AG'&=x+GG'\\
\\
&=\dfrac{2Mx+2mx+mL}{2(m+M)}.
\end{align*}
$$
Then, I observe that momentum in the system is conserved horizontally as there is no external horizontal force. Therefore,
$$
mv=(m+M)w\\
\text{ }\\
w=\dfrac{mv}{m+M},
$$
where ##w## is the velocity at which the center of gravity of the system will move after the block is given a velocity ##v##.
Next, I calculate the acceleration ##a## of the little block and get ##a=\dfrac{\mu mg}{m}=\mu g##.
If ##t## is the time that the block will take to come to rest, I have ##0=v-\mu gt##, so ##t=\dfrac{v}{\mu g}##.
If the distance that the center of gravity of the system moves in time ##t## is equal to ##AG'##, then the system will be at the verge of toppling over. Therefore,
$$
\begin{align*}
w\cdot t&=\dfrac{2Mx+2mx+mL}{2(m+M)}\\
\\
\dfrac{mv}{m+M}\cdot \dfrac{v}{\mu g}&=\dfrac{2Mx+2mx+mL}{2(m+M)}\\
\\
\dfrac{mv^2}{\mu g}&=\dfrac{2Mx+2mx+mL}{2}\\
\\
v^2&=\dfrac{\mu g}{2m}\cdot\left(2Mx+2mx+mL\right)\\
\\
v&=\sqrt{\mu g\left(x+\dfrac{L}{2}+\dfrac{Mx}{m}\right)}.
\end{align*}
$$
Is this correct?
Thank you very much for your assistance.
Isn't it so, that irrespective of the velocity given to the block, at some point both the rod and block will acquire equal velocities as a result of their acceleration and deceleration, and then just continue moving forward at that velocity?
If by any chance that were not the case, I tried solving it as follows.
First I calculate the distance to the center of gravity, say ##G'##, of the system from ##A##. We have
$$
GG'=\dfrac{m}{m+M}\cdot\dfrac{L}{2},
$$
and so we have
$$
\begin{align*}
AG'&=x+GG'\\
\\
&=\dfrac{2Mx+2mx+mL}{2(m+M)}.
\end{align*}
$$
Then, I observe that momentum in the system is conserved horizontally as there is no external horizontal force. Therefore,
$$
mv=(m+M)w\\
\text{ }\\
w=\dfrac{mv}{m+M},
$$
where ##w## is the velocity at which the center of gravity of the system will move after the block is given a velocity ##v##.
Next, I calculate the acceleration ##a## of the little block and get ##a=\dfrac{\mu mg}{m}=\mu g##.
If ##t## is the time that the block will take to come to rest, I have ##0=v-\mu gt##, so ##t=\dfrac{v}{\mu g}##.
If the distance that the center of gravity of the system moves in time ##t## is equal to ##AG'##, then the system will be at the verge of toppling over. Therefore,
$$
\begin{align*}
w\cdot t&=\dfrac{2Mx+2mx+mL}{2(m+M)}\\
\\
\dfrac{mv}{m+M}\cdot \dfrac{v}{\mu g}&=\dfrac{2Mx+2mx+mL}{2(m+M)}\\
\\
\dfrac{mv^2}{\mu g}&=\dfrac{2Mx+2mx+mL}{2}\\
\\
v^2&=\dfrac{\mu g}{2m}\cdot\left(2Mx+2mx+mL\right)\\
\\
v&=\sqrt{\mu g\left(x+\dfrac{L}{2}+\dfrac{Mx}{m}\right)}.
\end{align*}
$$
Is this correct?
Thank you very much for your assistance.
.
. It hasn't got to do anything with rolling.