walking
- 73
- 8
I am reading Tipler & Mosca 5th edition. On pages 289-290 there is an example problem which seems to assume that Newton's second law for torque works just as well when we apply it to the centre of mass of an object. However, before this example problem was introduced, the authors did not state anything about NII for centre of mass and only derived it for torques in general. After the example problem however, they seem to be saying that NII for torques does indeed work for centres of mass (see yellow box).
Here is the example problem:

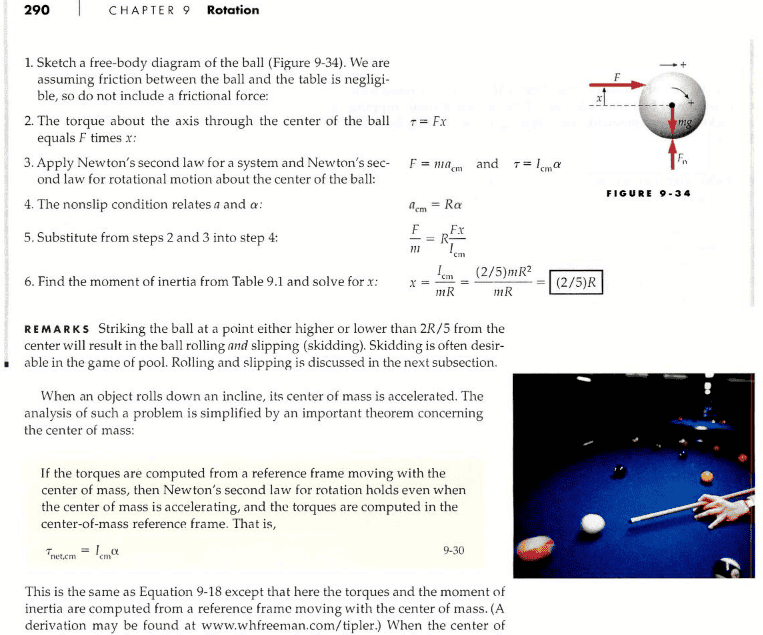
As you can see, in the problem they seem to assume that ##\tau_{net ext}=I\alpha## also holds as ##\tau_{cm}=I_{cm}\alpha##, at least for this particular problem. However, my problem is that they only state that it holds for centres of mass after the example problem, rather than before it. This makes me believe that I am missing something and maybe what they did is just a straightforward application of NII which I am not seeing? Maybe we do not need the theorem they state afterwards (in the yellow box) in order to solve the example problem as they solved it?
In any case, I think I have managed to prove that their application of NII-for-torques to centre of mass of the sphere is valid. Here is my proof:
If we apply NII without assuming it works for centre of mass, we have to use the fact that the ball rolls about an axis in contact with the ground (earlier in this chapter in the book it says that a rolling ball rolls about an axis on the ground). Since the radius of the ball is R, then applying NII for torques we get ##F(x+R)=I\frac{a}{R}## where ##a## is the tangential acceleration. Now by the parallel axis theorem, we have ##I=I_{cm}+MR^2## giving ##F(x+R)=(I_{cm}+MR^2)\frac{a}{R}##. Now by NII for linear motion, ##F=Ma## and so the last equation simplies to ##Fx=I_{cm}\alpha##, which is NII-for-torques applied to the centre of mass of the ball, as required.
Here is the example problem:
As you can see, in the problem they seem to assume that ##\tau_{net ext}=I\alpha## also holds as ##\tau_{cm}=I_{cm}\alpha##, at least for this particular problem. However, my problem is that they only state that it holds for centres of mass after the example problem, rather than before it. This makes me believe that I am missing something and maybe what they did is just a straightforward application of NII which I am not seeing? Maybe we do not need the theorem they state afterwards (in the yellow box) in order to solve the example problem as they solved it?
In any case, I think I have managed to prove that their application of NII-for-torques to centre of mass of the sphere is valid. Here is my proof:
If we apply NII without assuming it works for centre of mass, we have to use the fact that the ball rolls about an axis in contact with the ground (earlier in this chapter in the book it says that a rolling ball rolls about an axis on the ground). Since the radius of the ball is R, then applying NII for torques we get ##F(x+R)=I\frac{a}{R}## where ##a## is the tangential acceleration. Now by the parallel axis theorem, we have ##I=I_{cm}+MR^2## giving ##F(x+R)=(I_{cm}+MR^2)\frac{a}{R}##. Now by NII for linear motion, ##F=Ma## and so the last equation simplies to ##Fx=I_{cm}\alpha##, which is NII-for-torques applied to the centre of mass of the ball, as required.