Torque and forces (Beginner level)

[zimmer132123]

Summary:: I am trying to figure out how much force that either end of a tilted rod are subjected to as a consequence of gravity. One end being attached to a hinge, the other to a string from above.

Hello, it's my first time on this forum. I have recently started learning about torque (Nm) and i have encountered my first problem.

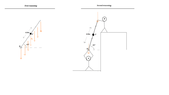
As described in the included picture, i want to figure out how one would calculate the forces that point H (hinge) and the string in the other end are subjected to in case 3.

I did some simple calculations as examples, just to show how i understand things so far:

- When a one-dimensional line is horizontal, like in case 1, calculating the forces at those points that "carries" the line seems straight forward.

- On to case 2, suppose the line is balanced vertically, point H will be subjected to the whole weight of 50 N and therefore i excluded the string.

- Now, having a tilted line that is held up by point H and the string in the other end, as in case 3, i just can't seem to figure out how to calculate the forces that these ends are subjected to?

I thought of using the same principle for calculating the force exerted on the string (Fb), as when calculating F1 and F2 using the torque-value, but it will always result in half the total weight → 25 N, no matter the tilt (Intuitively i figured this has to do with using the point mass in the torque calculation but I'm not sure why, and this is probably the deeper and perhaps mathematical knowledge that i am lacking).

So how do one go about this? To me it is obviously more force exerted on point H, until the line is tilted all the way down to a horizontal position as in case 1, where forces are equally distributed between the two ends.

Any answers are appreciated. Thanks

 

[jbriggs444]

This appears to be homework. I have made a request for it to be moved to a more appropriate sub-forum.

The problem appears to center on the third case, the rightmost in your drawing. Restating the problem:

A uniform rod is held in a diagonal orientation. It is supported at the lower left end by a hinge and at the upper right end by a vertical string. It is subject to a downward force from gravity.

The rod has a weight of 50 N. It is 4.0 meters in length. It is at an angle of 65 degrees from the horizontal.

What support force is required from the string to maintain the rod in this position?

but it will always result in half the total weight → 25 N

Bingo. There you have the correct answer. Now the only problem is working to properly justify it.

As drawn, you seem to have a vertical string producing a diagonal force. But that is not right. A vertical string always produces a vertical force.

It follows that there is no horizontal force from the string. Nor is there any horizontal force from gravity. So there can be no horizontal force from the hinge.

Conclusion: The force from the hinge must act vertically.

 

[BvU]

Hello @zimmer132123 ,

$\qquad$ !​

I think you do understand cases 1 and 2, so I'll focus on case 3.
A few things to consider in such cases:

• we consider static equilibrium, which means
• all forces (vectors!) add up to zero in any direction
• all torques (considered from any reference point) add up to zero

Furthermore:

• a taut string only exerts a force in a direction along the string

Generally, the balance of forces in 2 perpendicular directions yields 2 equations and the torque gives another one.

I am puzzled by your picture: I see forces $F_b$ and $F_a$ that compensate $F_s=50\; {\sf N}$.

I don't see what $F_1$ and $F_2$ have to do with anything. Where do they come from ? Why are they in the drawing ?

[edit]Ah, JB was a little faster...
$\$

 

[BvU]

Conclusion: The force from the hinge must act vertically.

Compare with the same situation, except that H is not a hinge but a resting point on a frictionless surface: any deviation from a vertical string would set the rod in motion, sideways.

$\$

 

[Lnewqban]

Welcome!
Why does the string disppeared in case #2?
It could be the case of a crane lowering a vertical bar to the ground.
There is a transition from all weight on the string to all weight on the lower end of the bar.

 

[jbriggs444]

There is a transition from all weight on the string to all weight on the lower end of the bar.

Statically indeterminate

 

[zimmer132123]

This appears to be homework. I have made a request for it to be moved to a more appropriate sub-forum.

The problem appears to center on the third case, the rightmost in your drawing. Restating the problem:

A uniform rod is held in a diagonal orientation. It is supported at the lower left end by a hinge and at the upper right end by a vertical string. It is subject to a downward force from gravity.

The rod has a weight of 50 N. It is 4.0 meters in length. It is at an angle of 65 degrees from the horizontal.

What support force is required from the string to maintain the rod in this position?Bingo. There you have the correct answer. Now the only problem is working to properly justify it.

As drawn, you seem to have a vertical string producing a diagonal force. But that is not right. A vertical string always produces a vertical force.

It follows that there is no horizontal force from the string. Nor is there any horizontal force from gravity. So there can be no horizontal force from the hinge.

Conclusion: The force from the hinge must act vertically.

What support force is required from the string to maintain the rod in this position?

Spot on.

Well, that the force that i am looking for acts vertically i do understand. I only made the two other diagonal calculations in case 3 for the sake of displaying how big the forces would have been, in case of a diagonal string.

So 25 N is correct? Let's say the rod is tilted less with an angle of 85 degrees from the horizontal plane, almost completely vertical. Using the same way of calculating, it will still result in 25 N. How is this right? To me it seems obvious that more force is exerted on H (hinge) and the supporting force acting vertically on the string would be lower?

 

[zimmer132123]

Hello @zimmer132123 ,

$\qquad$ !​

I think you do understand cases 1 and 2, so I'll focus on case 3.
A few things to consider in such cases:

• we consider static equilibrium, which means
• all forces (vectors!) add up to zero in any direction
• all torques (considered from any reference point) add up to zero

Furthermore:

• a taut string only exerts a force in a direction along the string

Generally, the balance of forces in 2 perpendicular directions yields 2 equations and the torque gives another one.

I am puzzled by your picture: I see forces $F_b$ and $F_a$ that compensate $F_s=50\; {\sf N}$.

I don't see what $F_1$ and $F_2$ have to do with anything. Where do they come from ? Why are they in the drawing ?

[edit]Ah, JB was a little faster...
$\$

I only made the two other diagonal calculations in case 3 for the sake of displaying how big the forces would have been, in case of a diagonal string. But i understand it might be misleading.

 

[zimmer132123]

Welcome!
Why does the string disppeared in case #2?
It could be the case of a crane lowering a vertical bar to the ground.
There is a transition from all weight on the string to all weight on the lower end of the bar.

I was trying to show how much force that H would be subjected to, in case the bar was "standing" on it, completely vertical. Since the total weight(force) of the bar would be on H, i excluded the string since the magnitude of the supporting force in the string would be zero.

 

[jbriggs444]

Using the same way of calculating, it will still result in 25 N. How is this right? To me it seems obvious that more force is exerted on H (hinge)?

Yes, still 25N.

Since both hinge and string are exerting forces that are purely vertical, this seems obvious. Perhaps you could share the reasoning that leads you to an opposing conclusion.

 

[jbriggs444]

I was trying to show how much force that H would be subjected to, in case the bar was "standing" on it, completely vertical. Since the total weight(force) of the bar would be on H, i excluded the string since the magnitude of the supporting force in the string would be zero.

In this situation, the total weight of the bar could be on H. The point is that it need not be.

 

[zimmer132123]

I want to thank everyone for their quick replies by the way.

I think i see your way of reasoning. Imagining several force vectors with a downwards vertical direction across the horizontal plane, for the x-distance of the bar. Since the rod is presumed to be homogenous, each of these vectors are of the same magnitude and equal forces would be exerted at any two points with equal distance from the object's center.

However, in reality, i feel that the lower supporting point will be subjected to a bigger force. In this included picture, my reasoning is that person A beneath the bar will experience more weight to push, compared to what person B will have to pull, in order for the bar to stay in its position (rest).

What am i missing?

 

[jbriggs444]

I do not see any reasoning in your reasoning. You've just put "I feel" in front of an unsupported assertion.

If the person up top is exerting a 25 N upward vertical force on the top end of the bar and the person down below is exerting a 25 N upward vertical force on the bottom end then their torques are in balance. The rod will not start rotating.

If they split the load 20/30 or 10/40 then the rod will be subject to an unbalanced net torque and will rotate.

If the bar is to be held in place with vertical forces, the torque balance requires that those forces must be equal.

The fellow up top could exert a small horizontal force to keep the rod in place and let the fellow down bottom provide all of the vertical support. If the two of them were carrying a sofa up the stairs, this is pretty much what one would expect the top guy to do. (For an 85 degree sofa, the top guy actually cheats best by exerting a force at 15 degrees above the horizontal). But that is not the situation at hand. In the situation at hand, the top guy is constrained to exert a purely vertical force.

There is actually nothing that stops the guy on the bottom from cheating with the sofa. He could let the top guy do all the heavy lifting while only providing a small force at 15 degrees above the horizontal away from the stairs. It's just that it's usually easier to push than to pull, so the bottom guy ends up carrying the bulk of the load.

 

[zimmer132123]

That's it, i am mixing rotational movement with the force of gravity. It's seems clear now. Your input is highly appreciated.

If i made the impression of being assertive in my posts, i would like to say that it is the complete opposite. I am fairly new to physics and i am just eager to learn.

Sincerely

 

[jbriggs444]

If i made the impression of being assertive in my posts

No, you were fine.