Dynamics problem (force and torque analysis) of a human finger

[ElectricVocaloid]

Homework Statement

Dynamics problem (force analysis) of the human finger, simulated with a motor that performs a torque pulling ideal strings

Relevant Equations

Dynamics problem (force analysis) of the human finger, simulated with a motor that performs a torque pulling ideal strings

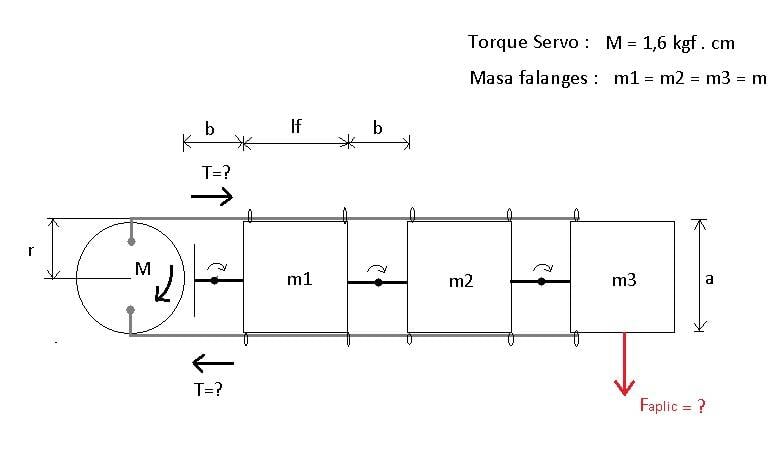
I was having trouble with a physics problem (string tension dynamics) In this case I have a model that simulates the phalanges of a human finger. Each phalanx is a block of mass m1, m2 or m3 respectively. And to simplify it, consider the 3 equal masses.

These phalanges are linked by joints that simulate the joints. attached to the upper and lower parts of the phalanges are 2 cords that join at each end of the phalanges, and then end by attaching to the ends of a rotary motor.

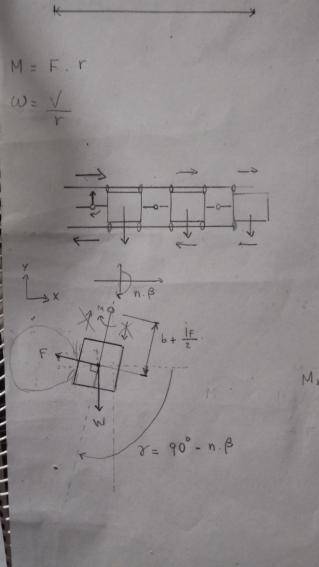
They give you the data of the torque M, of the lengths and of the masses, but you must know the tensions and the force that the fingertip (Faplic) would apply on a surface. Take into account that the movement is initiated by the torque M of the motor and is transmitted with the chains.

 

[Lnewqban]

Welcome!
Have you tried any solution yet?
We will need to know also the values of r, a, b and lf.
Note also that all these forces and moments are internal; something needs to restrict the mechanism from falling down on its own weight.

 

[ElectricVocaloid]

Welcome!
Have you tried any solution yet?
We will need to know also the values of r, a, b and lf.

I need to know the value of the Faplic indicated in red in the figure.
b is the length of half the joints and lf is the length of each phalanx (that is, of each square)
The distance on the X axis from the point of rotation of the motor to the point where this Faplic is: 2*b + lf + 2*b + lf + 2*b + lf/2
And the distance on the Y axis is a/2
Keep in mind that the weight of the raisin phalanx is:
Pf1 = m1 * g
Pf2 = m2 * g
Pf3 = m3 * g

Keep in mind that the chains simulate to be the muscles that move the bones, and they are ideal chains. In this case the finger is flexing upwards, meaning that F applied would be pointing upwards.

The values of:

r : radius of the circumference
a : finger height
b : joint segment length
lf : phalanx length (of each rectangle)

are all parameters that are assumed to be known, seeking to obtain a parameterized equation that relates the moment of the motor M with the force applied by the Faplic fingertip.

 

[ElectricVocaloid]

Welcome!
Have you tried any solution yet?
We will need to know also the values of r, a, b and lf.
Note also that all these forces and moments are internal; something needs to restrict the mechanism from falling down on its own weight.

As this simulates a real finger, the finger is attached to the hand, that is, the first of the joints is supporting the weight of the system, and the rotating cylinder is attached from its center to the axis of rotation of the motor that makes the torque M

 

[berkeman]

Welcome to PF.

I was confused by your figure at first, and I think I've figured it out but still have some questions. First, all of the rings on the masses that the strings pass through look like frictionless pass-throughs, but that can't be true of the last ones on m3. So maybe use 2 black dots instead of ring symbosl on m3 to indicate that the strings are attached to m3 at those two points.

And the other places where the strings are attached to m1 and m2 are frictionless ring pass-throughs, correct? Even if they are frictionless pass-throughs, they will still exert normal forces on the masses when the finger assembly bends, right? It would be good to draw the FBDs of all 3 of the masses at some point in the contraction of the finger assembly. From that you should be able to compute the forces at the 6 places on m1 and m2 and the 3 places on m3 to start getting you closer to calculating your circular actuator torque...

 

[ElectricVocaloid]

Welcome to PF.

I was confused by your figure at first, and I think I've figured it out but still have some questions. First, all of the rings on the masses that the strings pass through look like frictionless pass-throughs, but that can't be true of the last ones on m3. So maybe use 2 black dots instead of ring symbosl on m3 to indicate that the strings are attached to m3 at those two points.

And the other places where the strings are attached to m1 and m2 are frictionless ring pass-throughs, correct? Even if they are frictionless pass-throughs, they will still exert normal forces on the masses when the finger assembly bends, right? It would be good to draw the FBDs of all 3 of the masses at some point in the contraction of the finger assembly. From that you should be able to compute the forces at the 6 places on m1 and m2 and the 3 places on m3 to start getting you closer to calculating your circular actuator torque...

View attachment 304377

This exercise was copied from the pizzaron, I adapted it as best I could, but I forgot to indicate the last 2 rings differently, where the chains are attached.

The chains are attached to the sides of the cylinder and its other end is attached to the upper ring and the other to the lower ring of the last of the phalanges.

 

[berkeman]

So can you show a drawing of the finger assembly curled a bit and show all of the forces on each of the 3 blocks?

 

[ElectricVocaloid]

So can you show a drawing of the finger assembly curled a bit and show all of the forces on each of the 3 blocks?

If that torque continued for a while, the tensions of the chains would generate this effect on the fingers, the force of the fingertip would be the **Faplic**

 

[berkeman]

Nice! So now draw the 3 FBDs for the 3 masses in that position, and include the forces and angles, etc. You are well on your way to figuring this out!

 

[ElectricVocaloid]

Nice! So now draw the 3 FBDs for the 3 masses in that position, and include the forces and angles, etc. You are well on your way to figuring this out!

Try to divide it into 3 bodies (phalanges), assuming that the angles between the phalanges is a beta that is in the middle of each pair of phalanges.
The problem is that I cannot ensure that the moment in the engine cylinder is the same as in each joint, that is, how is M related to M3?
I understand that the chains link forces, but if that were the case, it could be against infinite phalanges and all of them could apply the same force F on their internal face.

 

[berkeman]

Sorry, your image is too low quality to help much. And you need to make your FBDs complete for each mass, which involves showing the forces at all 6 contact points on m1 and m2, and all 3 contact points on m3 (as well as the force due to gravity on each at their COM and the force on the final fingertip mass due to the load).

Do you have access to a scanner? If not, please work with your phone's flash and focus settings to improve your uploaded images. Thanks.

 

[ElectricVocaloid]

Sorry, your image is too low quality to help much. And you need to make your FBDs complete for each mass, which involves showing the forces at all 6 contact points on m1 and m2, and all 3 contact points on m3 (as well as the force due to gravity on each at their COM and the force on the final fingertip mass due to the load).

Do you have access to a scanner? If not, please work with your phone's flash and focus settings to improve your uploaded images. Thanks.

View attachment 304392

I'm sorry I don't have a good camera, that's why I was using digitally drawn diagrams, it's slower but it looks better.
What I was referring to is that I don't know if the moments M1, M2, M3 and M4 are equal, since if they are equal it means that each phalanx could make a force F equal to all the others, that is, they would be multiplying the forces by it number of phalanxes, which seems impossible to me because if there were infinite phalanges linked by the rope then there would be infinite forces (infinite force from a finite torque is impossible)

 

[berkeman]

I doubt that the torques are equal. I still need to see full FBDs for m1, m2 and m3 to be of any more help.

 

[ElectricVocaloid]

I doubt that the torques are equal. I still need to see full FBDs for m1, m2 and m3 to be of any more help.

this is the free body diagram for the original problem separating each of the elements.
There are several problems with this...

Are all torques equal to the torque that the motor makes?

All the forces that make the inner faces (the one that points down) of the phalanxes are equal? (to make it more understandable I suppose that the demo is wrapping an object)

 

[berkeman]

No. For m1 and m2 there are 6 force vectors acting on them. For m3 there are 3. Please show all of the force vectors for each FBD. Thank you.

 

[ElectricVocaloid]

No. For m1 and m2 there are 6 force vectors acting on them. For m3 there are 3. Please show all of the force vectors for each FBD. Thank you.

I think that there I have identified all the forces that act on each of the bodies that make up the system, is the diagram well done?

 

[berkeman]

The forces on the corners of m1 and m2 are normal to the masses, since those feed-throughs are frictionless, right?

 

[ElectricVocaloid]

The forces on the corners of m1 and m2 are normal to the masses, since those feed-throughs are frictionless, right?

They are assumed without friction. And the connecting chain is considered ideal because for the range of forces in which an average human finger would operate, therefore this chain that would represent the tensor muscle would not present deformations.

 

[berkeman]

Just because the hoops are frictionless, doesn't mean there is no normal force on them...

 

[ElectricVocaloid]

Just because the hoops are frictionless, doesn't mean there is no normal force on them...

Here I have clarified the normal forces (Fn) of each of the rings through which the binding chain passes.

 

[berkeman]

The forces on the attachment points on me will not be normal forces.

Okay, so given the angles in your diagram of the bent finger, can you post the equations for the sum of forces on each mass?

Please look at the Latex Guide link at the bottom of the Edit window to see how to post math equations. Thanks.

 

[ElectricVocaloid]

The forces on the attachment points on me will not be normal forces.

Okay, so given the angles in your diagram of the bent finger, can you post the equations for the sum of forces on each mass?

Please look at the Latex Guide link at the bottom of the Edit window to see how to post math equations. Thanks.

You better suggest using the flexed finger diagram or the extended finger diagram together in the instant before starting to flex ?

 

[Lnewqban]

View attachment 304367
As this simulates a real finger, the finger is attached to the hand, that is, the first of the joints is supporting the weight of the system, and the rotating cylinder is attached from its center to the axis of rotation of the motor that makes the torque M

That "T" connected to the extreme left pivot is a solid anchor to a fixed body.
A reaction force and moment to F aplicada at that point is what makes the existence of F aplic possible.
The motor must be also anchored to that fixed body for the mechanism to curl.

The curling happens because the tendon is restricted from moving away from the falanges; therefore, the above mentioned normal forces must exist.

How would you calculate F aplic for a simpler mechanism without falanges m1 and m2 and their pivots?

 

[ElectricVocaloid]

The forces on the attachment points on me will not be normal forces.

Okay, so given the angles in your diagram of the bent finger, can you post the equations for the sum of forces on each mass?

Please look at the Latex Guide link at the bottom of the Edit window to see how to post math equations. Thanks.

I have raised this study of forces for this system although I am not sure that it is right...

 

[ElectricVocaloid]

That "T" connected to the extreme left pivot is a solid anchor to a fixed body.
A reaction force and moment to F aplicada at that point is what makes the existence of F aplic possible.
The motor must be also anchored to that fixed body for the mechanism to curl.

The curling happens because the tendon is restricted from moving away from the falanges; therefore, the above mentioned normal forces must exist.

How would you calculate F aplic for a simpler mechanism without falanges m1 and m2 and their pivots?

The cylinder on which the chain is wound or released is connected from its center of rotation to a servomotor which, according to the data, performs a torque M = 1.6 kgf. cm

Since this system models a contracting finger linked to a hand, it can be seen that the first of the phalanges is linked to a "static wall" that would represent the hand.

This torque is quite weak for which it is valid to consider that the binding chain will not suffer deformations due to the tensions, for which it is considered an ideal chain. This chain is a way of modeling the tensor muscles that make the necessary torque so that our fingers can flex or extend depending on whether they are released from the inside and extended from the outside, or vice versa.

I have thought of not considering the first 2 phalanges, but the problem is that if I did not consider them, I would be stating that for an engine that generates 1.6 kgf. cm of torque it is the same to rotate 1 phalanx or 3 phalanges, or even infinite phalanges. I suppose that it is an inconsistency with the laws of energy conservation, because with a finite torque it would be generating infinite forces in all the buds (inner faces) of infinite phalanges linked by that ideal chain.

 

[haruspex]

attached to the upper and lower parts of the phalanges are 2 cords that join at each end of the phalanges, and then end by attaching to the ends of a rotary motor.

Two cords won't do it, and it is not how fingers work. E.g. in your diagram in post #8, m2 could twist back and forth with everything else staying (almost) still.
In the palm of the hand there are separate tendons for the three joints. See FDS and FDP tendons at https://www.assh.org/handcare/safety/tendons. Must be a third one for the joint at the palm.

 

[ElectricVocaloid]

Two cords won't do it, and it is not how fingers work. E.g. in your diagram in post #8, m2 could twist back and forth with everything else staying (almost) still.
In the palm of the hand there are separate tendons for the three joints. See FDS and FDP tendons at https://www.assh.org/handcare/safety/tendons. Must be a third one for the joint at the palm.

This design used in the problem emulates the fingers of the human being but this model is more used in robotics, the objective is to place a pressure gauge on the fingertips and check if the reaction force is greater or less than the Faplic. That is why Faplic is the unknown of this problem.

P = Fgauge / Afigertip

If (Faplic > Fgauge): touch object is deformable
If (Faplic == Fgauge): touch object is not deformable
If (Faplic > Fgauge): touch object is expanding

 

[haruspex]

This design used in the problem emulates the fingers of the human being but this model is more used in robotics, the objective is to place a pressure gauge on the fingertips and check if the reaction force is greater or less than the Faplic. That is why Faplic is the unknown of this problem.

P = Fgauge / Afigertip

If (Faplic > Fgauge): touch object is deformable
If (Faplic == Fgauge): touch object is not deformable
If (Faplic > Fgauge): touch object is expanding

View attachment 304416
View attachment 304417

Maybe the elasticity of the tendons somehow arranges that each joint bends through the same angle.

I think you can simplify a bit by taking the tension in one cord as zero. It is the difference in the tensions that matters,
It might be simplest to use virtual work. If the finger tip advances dx into the object, by how much does the length of the contracting tendon change?

Can you explain what's happening with the tendons in the bottom right image, Large grasp force, above? Looks like something is pulling the cords together.

 

[ElectricVocaloid]

Maybe the elasticity of the tendons somehow arranges that each joint bends through the same angle.

I think you can simplify a bit by taking the tension in one cord as zero. It is the difference in the tensions that matters,
It might be simplest to use virtual work. If the finger tip advances dx into the object, by how much does the length of the contracting tendon change?

Can you explain what's happening with the tendons in the bottom right image, Large grasp force, above? Looks like something is pulling the cords together.

I have simplified the problem to this study of forces.
A servomotor is attached to a cylinder that twists the thread on one side and releases it on the other.
This thread passes through some rings that are located in each of the ends of the phalanges and then they are tied in the last ring.
Between 2 phalanges there is a joint.
A servo motor creates a torque and generates the stresses, but many of those forces from the rigid body analysis will be internal forces since they cancel out.
The problem I'm having is that I can't think of a way to link the torque that the motor makes, with the force that the tip of the last of the phalanges can make on an object.

 

[haruspex]

I have simplified the problem to this study of forces.
A servomotor is attached to a cylinder that twists the thread on one side and releases it on the other.
This thread passes through some rings that are located in each of the ends of the phalanges and then they are tied in the last ring.
Between 2 phalanges there is a joint.
A servo motor creates a torque and generates the stresses, but many of those forces from the rigid body analysis will be internal forces since they cancel out.
The problem I'm having is that I can't think of a way to link the torque that the motor makes, with the force that the tip of the last of the phalanges can make on an object.View attachment 304418View attachment 304419

Did you try virtual work as I suggested?

 

[ElectricVocaloid]

Did you try virtual work as I suggested?

I've tried but I really can't find a way to fix it.I'm pretty lost with this problem.

And assuming that the torque of the servomotor is the same in all the joints, it seems to me that it is not correct because the number of phalanges on which it must act is an important factor to consider if I want to find the force in the tip of the last phalanx.

 

[haruspex]

I've tried but I really can't find a way to fix it.

Do what I said, use the geometry to figure out what a small advance dx of the finger tip corresponds to as a change in length of the contracting cord. Assume the angles are equal.

 

[ElectricVocaloid]

FINGER PAD CENTER (3 phalanges) = (dx, dy)

= ( ( 2b + lf ) . sen(β) + ( 2b + lf ) . sen(2β) + ( b + lf/2 ) . sen(3β) + a . sen(3β - 90°) ; ( b + ( 2b + lf ) . cos(β) + ( 2b + lf ) . cos(2β) - (b - l/2 ) . cos(3β) + a . cos(3β - 90°) )Here I have obtained the parameterized equation of the point where the fingertip would be...

and I need to conveniently transform the axes so that the positive y is up and the positive x is forward...

I was trying vector algebra to calculate at least the position of the point of the fingertip by linking it with the angle β of each joint.

 

[Lnewqban]

The cylinder on which the chain is wound or released is connected from its center of rotation to a servomotor which, according to the data, performs a torque M = 1.6 kgf. cm

Since this system models a contracting finger linked to a hand, it can be seen that the first of the phalanges is linked to a "static wall" that would represent the hand.

This torque is quite weak for which it is valid to consider that the binding chain will not suffer deformations due to the tensions, for which it is considered an ideal chain. This chain is a way of modeling the tensor muscles that make the necessary torque so that our fingers can flex or extend depending on whether they are released from the inside and extended from the outside, or vice versa.

I have thought of not considering the first 2 phalanges, but the problem is that if I did not consider them, I would be stating that for an engine that generates 1.6 kgf. cm of torque it is the same to rotate 1 phalanx or 3 phalanges, or even infinite phalanges. I suppose that it is an inconsistency with the laws of energy conservation, because with a finite torque it would be generating infinite forces in all the buds (inner faces) of infinite phalanges linked by that ideal chain.

We understand how the mechanism works.
Are you familiar with work and mechanical advantage concepts?
The number of falanges is irrelevant, higher number of those only makes the curve smoother.

Being an ideal mechanism, work in (tension tendon x tangential displacement) must be equal to work out (F apl x dispacement of finger's contact point).
There are axial forces on each falange and joint as reactions to the tension in the tendon; falanges here work as columns.

 

[ElectricVocaloid]

We understand how the mechanism works.
Are you familiar with work and mechanical advantage concepts?
The number of falanges is irrelevant, higher number of those only makes the curve smoother.

Being an ideal mechanism, work in (tension tendon x tangential displacement) must be equal to work out (F apl x dispacement of finger's contact point).
There are axial forces on each falange and joint as reactions to the tension in the tendon; falanges here work as columns.

taking into account that the first phalanx is attached to a static point that prevents it from falling (that is, the hand)... does the fact that there are more phalanges not imply that there is more weight that the chains must support when stretching or contracting?

all the phalanges in this problem we assume that they have the same length, which is lf, and we also assume that they all have the same mass, that is, their weights will be equal.

I am not sure that the torque M that the servomotor performs to rotate the cylinder is exactly the same as that experienced in the last of the joints...