Torque in one end of a rod in free space

[Mechanics89]

Hello.

I'm having trouble with determining the dynamics of a rod, when one of the ends has a torque applied to it. I've illustrated it in the figure below:

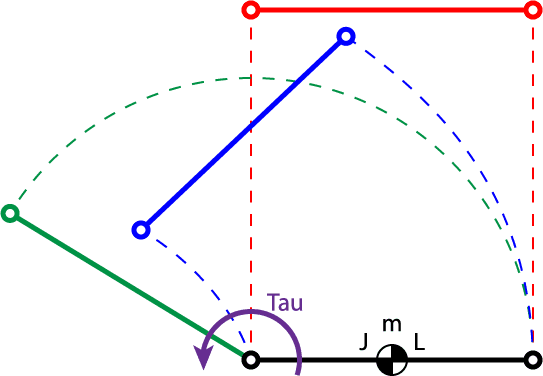
There are no external forces except of the torque - so no gravity, drag etc. Also, the rod is assumed rigid. How will it behave? Green, blue or red? And why?

Legend:
Tau (τ): Torque
m: Mass
J: Moment of inertia
L: Length

 

[Orodruin]

What is the net force on the rod? How is the center of mass going to move based on this?

 

[Mechanics89]

@Orodruin: I was thinking what there will be a force on the center of mass as the torque would imply this due to Tau = a x F?

 

[A.T.]

@Orodruin: I was thinking what there will be a force on the center of mass as the torque would imply this due to Tau = a x F?

You have to make up your mind, if there is just a external torque, or also external net force. If there is just a torque, then all forces "implied" by it cancel, and the COM won't accelerate.

 

[Mechanics89]

You have to make up your mind, if there is just a external torque, or also external net force. If there is just a torque, then all forces "implied" by it cancel, and the COM won't accelerate.

But why would the torque cancel out? The example should be thought of as no external net force is applied. Can it be explained by the following sketch, where the torque couples cancel out?:

I'm trying to determine the acceleration of the COM along with the angular acceleration around the COM.

 

[Doc Al]

But why would the torque cancel out?

The torque doesn't cancel, but the forces do. There is a torque, but no net force. No net force implies no acceleration of the COM.

 

[Mechanics89]

The torque doesn't cancel, but the forces do. There is a torque, but no net force. No net force implies no acceleration of the COM.

Okay, thanks. But the torque will imply an angular acceleration? Calculated by Tau = (I_COM + m * (L/2)^2) * Alpha? And will this angular acceleration be around the end or the COM?

 

[A.T.]

And will this angular acceleration be around the end or the COM?

If the COM cannot accelerate, can the rod rotate around the end?

 

[Mechanics89]

If the COM cannot accelerate, can the rod rotate around the end?

Nope - so will the acceleration be:

d2x = 0;
d2y = 0;
d2Phi = Tau / I_COM;

or:

d2x = 0;
d2y = 0;
d2Phi = Tau / (I_COM + m * (L/2)^2);

Or an I completely off track here? :)

 

[pranav_bhrdwj]

Hello,
I am unable to understand your figure. You have depicted that a torque acts about the 'end point' to the left however there is NO external force. A torque without the presence of forces imply the formation of a 'couple' in order to cancel out the forces. If that is the case, i cannot understand where the Couple forces must have been applied to produce a torque around the end point as depicted in the figure ! The way i see it, there must have been a force on the rod to produce a torque as shown.

 

[Orodruin]

Nope - so will the acceleration be:

d2x = 0;
d2y = 0;
d2Phi = Tau / I_COM;

or:

d2x = 0;
d2y = 0;
d2Phi = Tau / (I_COM + m * (L/2)^2);

Or an I completely off track here? :)

There is a way relating the torque around one point with the torque around another point if you know the force acting on the object and its point of application. What does that relation tell you in the case the total external force is zero?

 

[Mechanics89]

There is a way relating the torque around one point with the torque around another point if you know the force acting on the object and its point of application. What does that relation tell you in the case the total external force is zero?

That there is no torque as the total external net force is zero? :)

 

[Mechanics89]

Hello,
I am unable to understand your figure. You have depicted that a torque acts about the 'end point' to the left however there is NO external force. A torque without the presence of forces imply the formation of a 'couple' in order to cancel out the forces. If that is the case, i cannot understand where the Couple forces must have been applied to produce a torque around the end point as depicted in the figure ! The way i see it, there must have been a force on the rod to produce a torque as shown.

Okay, thanks for the answer. But for instance: assume a robotic arm with a single joint between two "bones". When the robotic joint is actuated, isn't there only a torque imposed in the joint, thus causing the arm to move? Or will the arm only be able to move, if a "muscle" is connected a small distance from the joint, thus making a nonzero total net force?

 

[Orodruin]

You can have a torque with total external force zero, you just need forces with different points of application but with the same magnitude.

However, when you have zero net force, the torque is the same regardless of which point you are considering (exercise: prove this!). Your problem is therefore equivalent to no net force and the same torque around the CoM.