Torque required to rotate steel pipe on rollers

[Rocket795]

Hello,

I'm stuck on what should be a fairly simple problem. Trying to calculate the size of motor required to rotate steel pipe at 0.33RPM around its axis, on 2 sets of rollers, 4 wheels total (hard rubber).

Pipe
48" OD Mild Steel pipe 0.5WT
24m in Length

Rollers
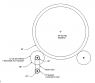
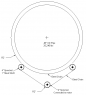
4 x 12" Rubber wheels (40" Center to Center) on bearings




This is where is stand.

Torque required to accelerate the system (0.00 RPM to 0.33 RPM in 1 sec)

Ta=Iα

I=(∏/32)ρL(D1^4-D2^4)

1.219 D1 – External diameter of the disc [m]
1.194 D2 – Internal diameter of the disc [m]
7,850.000 ρ – Density of the load [kg/m3]
9,069.050 m – Weight of the load [kg]
24.000 L – Length of the load [m]

I=3,300.689

α=(w1-w0)/t

0.000 ω0 – Initial velocity of the motor [rad/s]
0.035 ω1 – Final velocity of the motor [rad/s] or 0.33 RPM
1.000 t – Time for velocity change

α=0.035

Ta=114.064 N*m

Now the next part i am not too sure about,

Torque required to overcome rolling resistance :

Rolling resistance coefficient - f = 0.0077m Hard Rubber on Steel

http://www.roymech.co.uk/Useful_Tables/Tribology/co_of_frict.htm

F = f x W/R


Fr=(0.0077m*9069.050kg*9.81 kg/s^2)/0.610m

Trr= 1123.031 N *.610m = 685.049 N*m

Total Torque required to rotate the pipe at 0.33rpms in 1 sec.

T=Ta+Trr=799 N*m

or

589 Lb*ft

This seems low to me and this is only the torque at the pipe, once geared that torque will be significantly lower. will I know I'm missing the bearing friction torque required but that can't be that much.

What else should I be calculating?, if anything.

I have attached a drawing of the system, once I find the torque required for rotate the pipe I should have the required input torque dividing that Torque by the gear ratios.

One more thing, Bonus question. Some of these types of pipe have a seam welded down the middle along the length of the pipe, it projects from the pipe a few mm sort of like a speed bump on the pipe. Is there a way to calculate the torque required to over come the rollers once the seams comes in contact with the roller wheels?

Thanks in advance.

 

[Baluncore]

The initial torque to accelerate the rotation will be the most significant power requirement. Only once the speed has begun to pick up will frictional losses need to be overcome and they will be small in comparison to the initial breakaway at the start.

Now that bonus question. The seam can be a real problem because, if it is not pressed into the rubber roller, it will require the pipe to rise by more than the seam's height, and it will do it twice per turn. Lifting the pipe and then dropping it will cost energy. I have had problems while cutting pipe supported on rollers where the seam has stalled rotation, but I was using steel driving rollers. There are several potential ways to reduce the problem.

1. Removing the seam with a grinder works, it is quick and dirty, not a nice solution.

2. Use bigger diameter rollers with softer rubber that will accommodate the seam.

3. Separate or stagger the rollers by a different angle at each end so as to halve the number of energetic climbs. When the seam is climbing onto the roller at one end it is coming off at the other so some energy is recovered.

4. Make your rollers with many smaller free peripheral rollers, like a needle bearing. When the needles are pushed together there should be one gap between the end needles wide enough to accommodate the seam. The pipe can then roll on the combination of roller and needles, so the pipe seam will be accommodated between the needles when required as it passes a roller.

5. Use a belt or a chain loop around the rollers to cradle the pipe. One or more additional rollers will be needed below to keep the lowest loop of belt clear of the upper cradle. The belt should be tight enough to position the pipe, but loose enough so the seam does not suddenly lift the pipe significantly. The high frequency Fourier components of the seam are being reduced to a fundamental by the running average low pass belt filter.

 

[Baluncore]

The belt or chain loop technique has a 3 : 1 advantage over the 4” sprocket driving a 12”, surface contact roller. See attached sketch.

 

[Rocket795]

Thanks for your reply's Baluncore,

Perfect, I really like the idea of staggering the rollers and will probably go with a bigger diameter roller to accommodate. The belt chain chain system looks like it would be ideal, however the issue we run into is the we would have to accommodate different diameter pipes, from 12" up to 48" possibly bigger, with predetermined spacing.

But having a combination of softer rubber, staggered rollers, and 14" dia rollers should do the trick.

Do you think in this system grade resistance (Gr= m*g*sin(alpha) play a part, My thinking is that when the wheels are spaced further apart there is more torque required to turn them, but the trade off would be increased friction?

 

[Baluncore]

I see security of the 10 tonne mass being supported as the critical parameter in deciding alpha, with friction and torque being consequences of the required security. If the wheels are too far apart there will be a significantly greater force trying to spread the support rollers. That force may be momentarily increased by the passage of the seam or by a harmonic variation of a pipe's radius.

With a chain loop cradle, one of the rollers could be supported on a swing arm from below so as to adjust automatically to the pipe diameter. The pipe mass would be supported close to vertically by the chain loop while the idler rollers were pulled against the pipe by the chain loop, that is quite different to the simple roller pair analysis. If necessary the effective length of the chain could be changed by providing an alternative path length near the motor drive sprocket.