SUMMARY
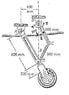
The discussion focuses on calculating the torque (T) required to lift a retracting nose wheel assembly at a 30-degree angle. The assembly has a combined mass of 50 kg, with the center of mass located at point G. The torque applied to arm BC generates a force at point C, which must be resolved into components acting along arms AG and CD to determine the necessary lifting force. The solution involves analyzing the forces and torques around point A to ensure the applied torque overcomes the gravitational force acting on the mass.
PREREQUISITES
- Understanding of torque and its application in mechanical systems
- Knowledge of vector decomposition in physics
- Familiarity with the principles of static equilibrium
- Basic concepts of mass and center of mass in mechanics
NEXT STEPS
- Study the principles of torque in mechanical systems
- Learn about vector decomposition and how to resolve forces
- Research static equilibrium conditions and their applications
- Explore the calculation of center of mass in composite bodies
USEFUL FOR
Mechanical engineers, physics students, and anyone involved in the design and analysis of mechanical systems requiring torque calculations.