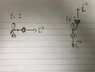- #1
Ayandas1246
- 2
- 0
List of relevant equations:
Angular Momentum = L (vector) = r(vector) x p(vector)
Angular velocity of rotating object = w(vector), direction found using right hand rule. Torque = T(vector) = dL(vector)/dt
I have a few questions about torque and angular momentum direction and conservation. The first has to do with an expanding Pizza dough which stretches after being tossed in the air. If I analyze a point mass on the outer edge of the dough, assuming the dough stays perfectly flat, is it safe to say that although the angle between the linear momentum vector and the r vector from the origin (the center of mass of the dough) is not 90 degrees, L still points in the same direction as w? Is it correct to say that L will only not point in the same direction as omega if the dough edge folds up or down as the dough spins and expands? My second set of questions pertains to the case in which we stand on a platform free to rotate and hold a rotating bicycle wheel then lift the wheel. (See attached file)
As drawn in the image, the system begins with some horizontal angular momentum L and a vertical angular momentum of zero. So in order for vertical angular momentum to be conserved between ti and tf, the person and platform must rotate with a downward angular momentum of magnitude L. But what about horizontal angular momentum? Was it not conserved? Additionally, when analyzing the same system using torque, why does the direction of the torque dictate the direction of the motion? If the wheel is raised between ti and tf, the direction of the force vector is determined by the direction of the change in angular momentum, which is straight up. So the force is pointed up, and by the right-hand rule, the torque points out of the page. But why is this the direction of motion? If we held a fishing rod instead of a spinning wheel, our force would point up and the torque we exert on the fish at the end of the rod would point out of the page, but the fish would move in an arc above us! Not into the page. Why does the wheel's angular momentum cause this motion in the direction of the torque? Finally, if the person were to start at ti with the wheel above their head (facing up) with zero angular momentum, then spin it such that at tf the wheel has an angular momentum of magnitude L pointing up, why wouldn't the platform and person move to compensate, resulting in a balancing L that points down? Wouldn't angular momentum in the vertical direction need to stay at zero? Apologies for the deluge of questions, and thank you tremendously for your help!
Angular Momentum = L (vector) = r(vector) x p(vector)
Angular velocity of rotating object = w(vector), direction found using right hand rule. Torque = T(vector) = dL(vector)/dt
I have a few questions about torque and angular momentum direction and conservation. The first has to do with an expanding Pizza dough which stretches after being tossed in the air. If I analyze a point mass on the outer edge of the dough, assuming the dough stays perfectly flat, is it safe to say that although the angle between the linear momentum vector and the r vector from the origin (the center of mass of the dough) is not 90 degrees, L still points in the same direction as w? Is it correct to say that L will only not point in the same direction as omega if the dough edge folds up or down as the dough spins and expands? My second set of questions pertains to the case in which we stand on a platform free to rotate and hold a rotating bicycle wheel then lift the wheel. (See attached file)
As drawn in the image, the system begins with some horizontal angular momentum L and a vertical angular momentum of zero. So in order for vertical angular momentum to be conserved between ti and tf, the person and platform must rotate with a downward angular momentum of magnitude L. But what about horizontal angular momentum? Was it not conserved? Additionally, when analyzing the same system using torque, why does the direction of the torque dictate the direction of the motion? If the wheel is raised between ti and tf, the direction of the force vector is determined by the direction of the change in angular momentum, which is straight up. So the force is pointed up, and by the right-hand rule, the torque points out of the page. But why is this the direction of motion? If we held a fishing rod instead of a spinning wheel, our force would point up and the torque we exert on the fish at the end of the rod would point out of the page, but the fish would move in an arc above us! Not into the page. Why does the wheel's angular momentum cause this motion in the direction of the torque? Finally, if the person were to start at ti with the wheel above their head (facing up) with zero angular momentum, then spin it such that at tf the wheel has an angular momentum of magnitude L pointing up, why wouldn't the platform and person move to compensate, resulting in a balancing L that points down? Wouldn't angular momentum in the vertical direction need to stay at zero? Apologies for the deluge of questions, and thank you tremendously for your help!