Torsion and deflection of a rectangular beam

[dbag123]

Homework Statement

calculate the total displacement of the angled part. deflection and torsion

Relevant Equations

-

Hello
I would like some feedback about a problem. The idea is to calculate how much the angled bit of this beam moves things to account for are deflection and torsion. Did i miss anything?

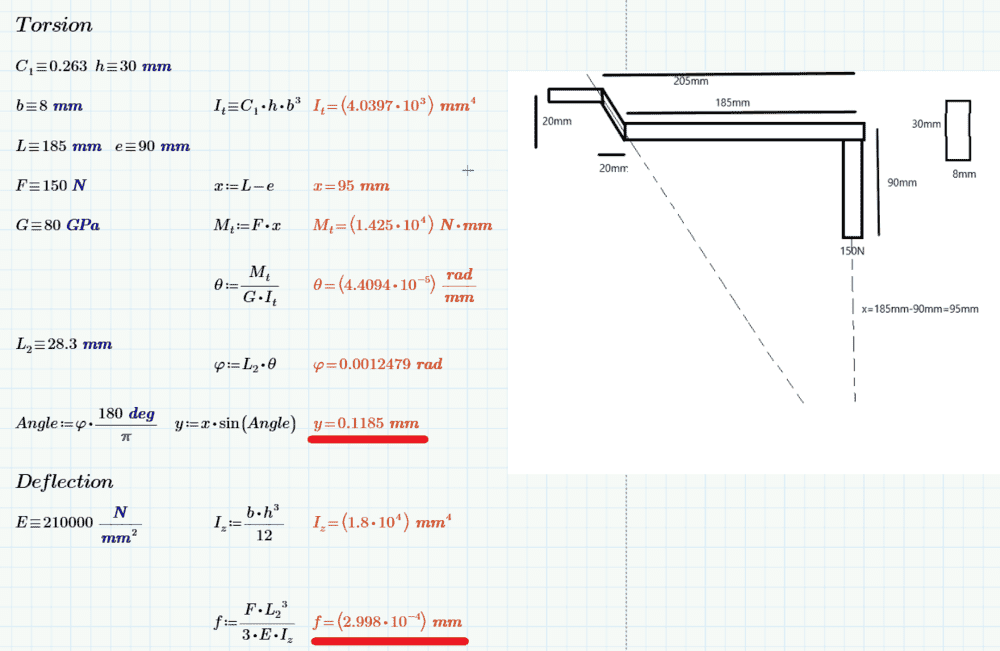
Underlined with red are the displacements in millimeters.

In the picture the dotted line is the axis that the beam twists about.

 

[dbag123]

I_t= torsion constant
M_t= Moment caused by torsion
Theta = torsion of the profile in rad for every mm
Phi = Total amount of torsion for the section
y= displacement caused by torsion

 

[PhanthomJay]

I don’t know where you are getting values for e and x. Please explain.

 

[dbag123]

e = the length of the handle (90mm)

x = the leftover distance. (triangle side b-handle=95mm)
The angle of the bend is 45deg, so those 2 sides of the imaginary triangle are both 185mm, so 185mm-90mm(handle) = 95mm

 

[PhanthomJay]

I still don’t get it , especially the direction of the handle. Is it like this thread you posted last week?
https://www.physicsforums.com/threa...tional-area-for-strength.977892/#post-6238482

 

[dbag123]

yes, same object different problem

 

[dbag123]

I still don’t get it , especially the direction of the handle. Is it like this thread you posted last week?
https://www.physicsforums.com/threa...tional-area-for-strength.977892/#post-6238482

3D-picture of it

 

[PhanthomJay]

Let the x-axis be horizontal, y-axis vertical, and z axis out of plane in direction of handle. The load F is applied vertically down along y axis. I thought we agreed for torsion at say the fixed end the torsion moment is Fz = 150 (110), right?

 

[dbag123]

that is true, for torsion at point of rotation (fixed point). However the perpendicular distance to the acting force in this case(looking at the angled part only) according to my calculation should be 95mm, and the torsion moment 150(95)

The total deflection of this angled bit should be very small, and i know that deflection due to anything has a lot to do with the length of the object being bent

 

[PhanthomJay]

Oh, the angled beam, OK, but you are not calculating the torsion on the angled beam correctly. If you extend the longitudinal axis of the angled beam (as you have done , making it the hypotenuse of the 185/185 legs), then the torsion on the angled beam is the Force of 150N times the perpendicular distance from that force to the extended angle beam axis, which I calculate as (150)(95)/SQRT 2.

 

[dbag123]

Oh, the angled beam, OK, but you are not calculating the torsion on the angled beam correctly. If you extend the longitudinal axis of the angled beam (as you have done , making it the hypotenuse of the 185/185 legs), then the torsion on the angled beam is the Force of 150N times the perpendicular distance from that force to the extended angle beam axis, which I calculate as (150)(95)/SQRT 2.

do you mean like this?

the x distance?

 

[PhanthomJay]

Yes!

 

[dbag123]

Allright. what about the displacement in mm? y=x*sin(angle), I am guessing the x distance also changes from 95 to 67,2mm

 

[PhanthomJay]

my brain is getting fried with this problem.

The deflection from bending moments in the angled beam is more than PL^3/3EI, because there is also a bending moment couple applied at the end where you are calculating the deflection.
Now there's twisting going on all over the place, much of it just rotating the beam section without vertical deflection, but I think that vert deflection in the angled beam from twisting moments is governed by the twist angle at the critical section at the cantilever end, which can be ignored since it is small. I'd have to think more about this while you do the same.