Total force generated in a pneumatic cylinder-piston with kn

Click For Summary
SUMMARY

The discussion focuses on modeling the total steady-state force generated by a pneumatic cylinder-piston system, specifically in the presence of leakage. The equation sought is in the form of \( F = f(P_1, A, L, c) \), where \( P_1 \) is the pressure, \( A \) is the surface area, \( L \) is the length, and \( c \) is the clearance. In extreme cases, the force can be approximated as \( F = P_1A \) for negligible clearance and \( F \approx \frac{1}{2}\rho\nu^2C_DA \) for larger clearances. The discussion also highlights the importance of calculating the pressure \( P_0 \) during transient conditions using standard air flow methods.

PREREQUISITES
  • Understanding of pneumatic systems and cylinder-piston mechanics
  • Knowledge of fluid dynamics, specifically air flow calculations
  • Familiarity with empirical and theoretical models for leakage
  • Basic grasp of hydrostatic pressure and drag force concepts
NEXT STEPS
  • Research pneumatic cylinder-piston design principles and performance metrics
  • Study fluid dynamics equations related to air flow and leakage in pneumatic systems
  • Learn about empirical models for calculating leakage in pneumatic applications
  • Explore the effects of clearance on pneumatic system efficiency and performance
USEFUL FOR

Engineers, mechanical designers, and researchers involved in pneumatic system design and optimization, particularly those focusing on force generation and leakage management in cylinder-piston configurations.

foadsf
I have also asked this question in SO and CFD online

Assuming that we have a pneumatic cylinder-piston with arbitrary but known surface area A, a known clarence c, and a known length L. What is the best model to describe the total steady state force applied on the piston considering the leakage? (the force required to keep the piston in place)

Bn1if.png
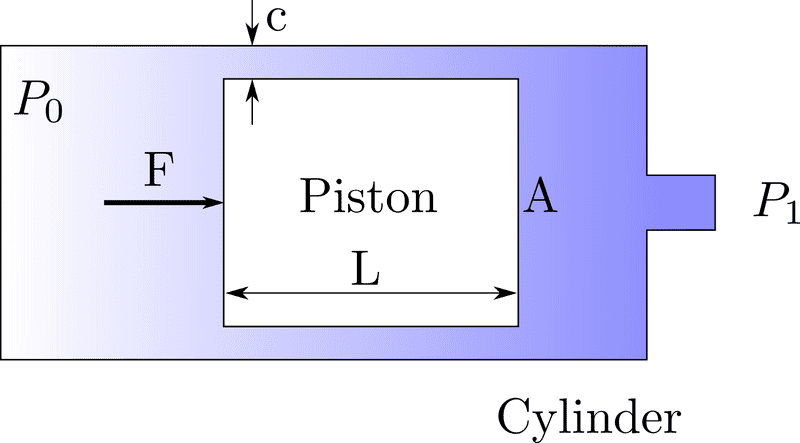What I'm looking for is an equation in the form of $F=f\left(P_1,A, L, c\right)$. In extreme cases:

- if ## c\rightarrow 0 ## then ##F=P_1A## is just hydrostatic pressure
- if c is big then ##F\approx \frac{1}{2}\rho\nu^2C_DA## is just air drag

I can calculate leakage from empirical or theoretical models but I don't know how to proceed from there.
 

Attachments

  • Bn1if.png
    Bn1if.png
    17.8 KB · Views: 639
Physics news on Phys.org
Given that the piston is not moving and that there is at least some leakage of air possible around the piston then :

When the system is in steady state condition P0 = P1 and F = 0

When the system is in transient condition P0 is initially < P1 but increases with time as air flows around the piston . To a good approximation at any time t during this transient period F = (P1 - P0 at time t) x A .

The value of P0 at time t can be determined using standard air flow calculation methods .

You could calculate the viscous air drag force on the piston at time t as well but it is likely to be insignificant in many practical cases .
 
Last edited:

Similar threads

Calculating Fluid Dynamic Forces on a Towing Cable
  • · Replies 3 ·
Replies
3
Views
4K