- #1
Ocata
- 198
- 5
This homework problem was originally posted in another forum so there is no template
Suppose a block of 5kg is stationary on a table with [itex]μ_{s} = .15 [/itex] and [itex]μ_{k} = .1 [/itex]
[itex]μ_{s}(F_{N}) = μ_{s}(mg)= .15(5)(10\frac{m}{s^{2}}) [/itex] =7.5N
[itex]μ_{k}(F_{N}) = μ_{k}(mg)= .1(5)(10\frac{m}{s^{2}}) [/itex] = 5NThe force applied to the block is represented by the function:
[itex] f(x) = 7.5Sin(\frac{π}{10}x) [/itex]
Where at time t = 5, static friction is broken and at time t = 7.67, equilibrium is reached, and at time t = 10, force is no longer applied.
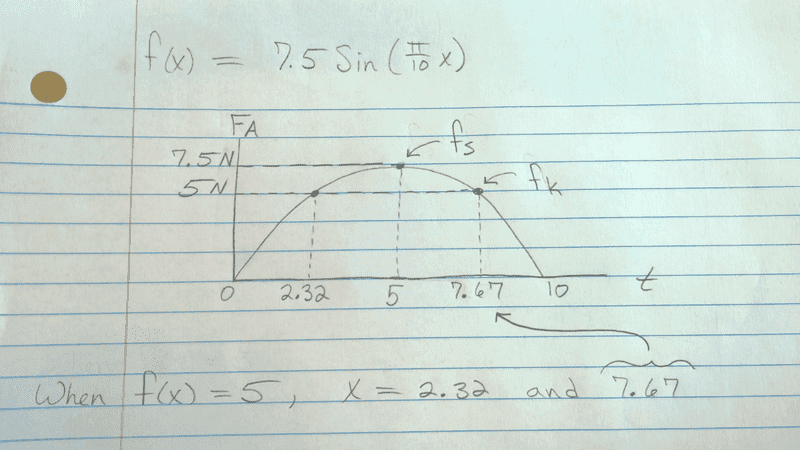 Taking into account kinetic friction is 5N, I am imagining that from time t = 0 to t = 5, the 5kg block does not move even though there is an increasing force applied to it.
Taking into account kinetic friction is 5N, I am imagining that from time t = 0 to t = 5, the 5kg block does not move even though there is an increasing force applied to it.
Once the force applied to the block reaches 7.5N (which occurs at time t = 5), the Net Force on the block is [itex]Fnet = 7.5N - μ_{s}(F_{N}) = 7.5N - 5N = 2.5N[/itex]
It just so happens that as static friction is broken at applied force of 7.5N, the force applied to the block begins to decrease.
I imagine that a graph of the Net Force on the block would like exactly like this:
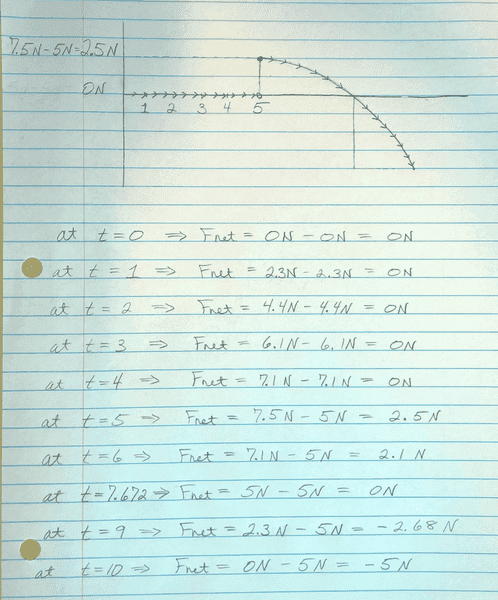
Which I would describe as piecewise function like this:
[itex] y = 0 [/itex] from time t(0,5)
[itex] 7.5Sin((\frac{π}{10})x) -5 [/itex] from time t(5,10)
Now my goal right now is to be able to calculate the correct Impulse experienced by the block from time t(0,10).Question 1: Is there an impulse on the block between time 0s and 5s, which the block is stationary due a max 7.5N of static friction?
Question 2: The impulse on the block between the time 5s and 7.672s seems to be 4N as described here:
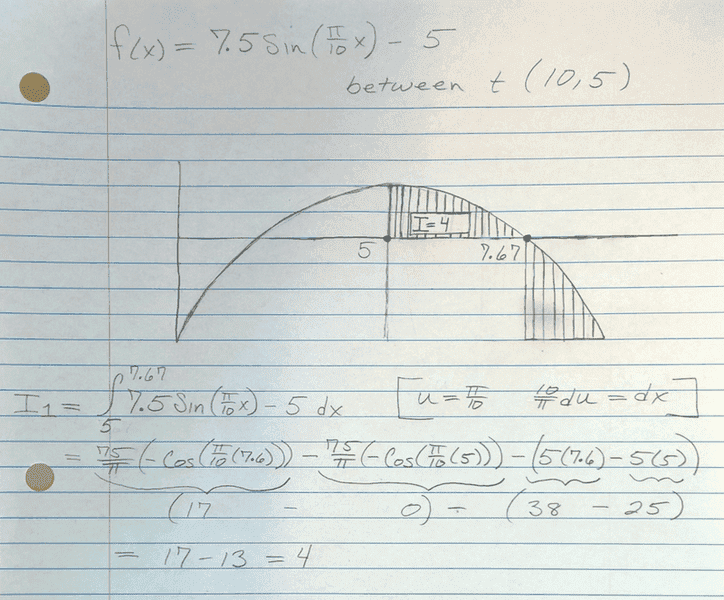
However, to calculate the impulse between time 7.67s and 10s, I don't know how I should be considering the area under the curve. I guess it would be one of either two ways as illustrated here:
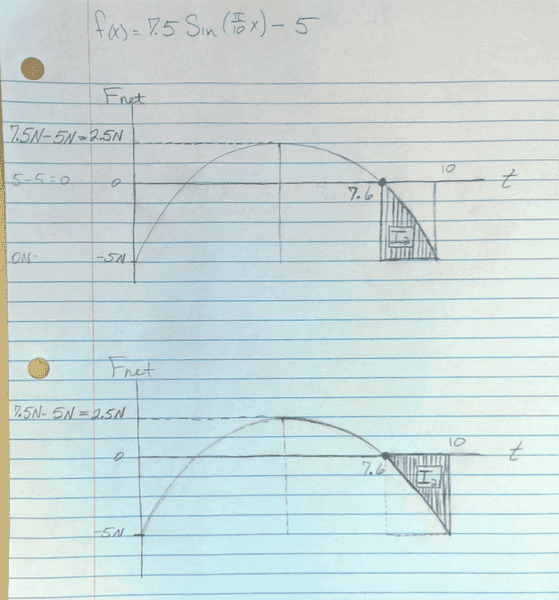
Question 3:
Does the block actually stop moving before 10 seconds?
How can I know when this happens?
Question 4:
Can I only calculate an accurate impulse value once I first calculate the time at which the block is not longer moving? This may go back to question one: Does impulse on the block occur when a force is applied to the block even when the block remains stationary due to friction?
Thank you
[itex]μ_{s}(F_{N}) = μ_{s}(mg)= .15(5)(10\frac{m}{s^{2}}) [/itex] =7.5N
[itex]μ_{k}(F_{N}) = μ_{k}(mg)= .1(5)(10\frac{m}{s^{2}}) [/itex] = 5NThe force applied to the block is represented by the function:
[itex] f(x) = 7.5Sin(\frac{π}{10}x) [/itex]
Where at time t = 5, static friction is broken and at time t = 7.67, equilibrium is reached, and at time t = 10, force is no longer applied.
Once the force applied to the block reaches 7.5N (which occurs at time t = 5), the Net Force on the block is [itex]Fnet = 7.5N - μ_{s}(F_{N}) = 7.5N - 5N = 2.5N[/itex]
It just so happens that as static friction is broken at applied force of 7.5N, the force applied to the block begins to decrease.
I imagine that a graph of the Net Force on the block would like exactly like this:
Which I would describe as piecewise function like this:
[itex] y = 0 [/itex] from time t(0,5)
[itex] 7.5Sin((\frac{π}{10})x) -5 [/itex] from time t(5,10)
Now my goal right now is to be able to calculate the correct Impulse experienced by the block from time t(0,10).Question 1: Is there an impulse on the block between time 0s and 5s, which the block is stationary due a max 7.5N of static friction?
Question 2: The impulse on the block between the time 5s and 7.672s seems to be 4N as described here:
However, to calculate the impulse between time 7.67s and 10s, I don't know how I should be considering the area under the curve. I guess it would be one of either two ways as illustrated here:
Question 3:
Does the block actually stop moving before 10 seconds?
How can I know when this happens?
Question 4:
Can I only calculate an accurate impulse value once I first calculate the time at which the block is not longer moving? This may go back to question one: Does impulse on the block occur when a force is applied to the block even when the block remains stationary due to friction?
Thank you
Last edited:
