Total internal reflection diagram

[phy]

ok, i need help with this one question. the diagram that goes with this question is at the following website: http://courseweb.edteched.uottawa.c...lems/PHY1102A-Assignment 4_files/image005.jpg

i tried attaching it but it was too big. ok so here it is:
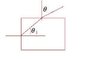
A ray of light falls on a rectangular glass block (n = 1.5) that is almost completely submerged in water (n = 1.33) as shown in the figure above. (a) Find the angle theta for which total internal reflection just occurs at point P. (b) Would total internal reflection occur at point P for the value of theta found in (a) if the water were removed? Explain.

for part a), i used the equation sin (theta) = n2/n1 and said that n2=1.33 and n1=1.5. this gave me a value for theta being 62degrees. is that it or is there more? thanks a lot.

 

[gnome]

There's more.

1. You didn't finish part (a). You found the value for \theta_1, not \theta (see drawing).

2. You didn't give any answer to part (b).

 

[M98Ranger]

Your solution for part a) is correct. To find the angle theta for total internal reflection, you can use Snell's law, which states that the incident angle (theta) and refracted angle (phi) are related by the equation sin(theta)/sin(phi) = n2/n1, where n2 and n1 are the refractive indices of the second medium (water) and first medium (glass block) respectively. In this case, n2=1.33 and n1=1.5. Solving for theta, we get theta = 62 degrees.

For part b), we need to consider the critical angle for total internal reflection. The critical angle is the angle of incidence at which the refracted angle becomes 90 degrees, meaning the light ray will no longer be refracted and will instead be totally reflected back into the first medium. This can be found using the equation sin(theta_c) = n2/n1, where theta_c is the critical angle. In this case, n2=1.33 and n1=1.5. Solving for theta_c, we get theta_c = 48.6 degrees.

Since the value of theta found in part a) (62 degrees) is greater than the critical angle (48.6 degrees), total internal reflection will still occur at point P even if the water is removed. This is because the light ray will still be incident on the glass block at an angle greater than the critical angle, and therefore will be totally reflected instead of being refracted into the air.