Total magnetic moment of hydrogen in weak magnetic field

[Trettman]

"Calculated the total magnetic moment of a hydrogen atom in the ground state in a weak magnetic field which arises from hyper fine splitting of the ground state. How many beams does hydrogen produce from a Stern-Gerlach analyzer with a weak magnetic field?"

I've calculated the magnetic moments from the hyper fine structure splitting to be

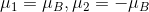
but I don't really know how to get the total magnetic moment of hydrogen. My guess so far is to compute the vector sum of

• the electron's spin magnetic moment
• the electron's orbital magnetic moment
• the proton's spin magnetic moment
• the magnetic moment that arises from the hyper fine structure (
  
  ),

but I have no idea where

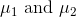"point". How do you "vectorize" them?

I'm also kind of confused as to how the magnetic moment of a particle is calculated. For example, the spin magnetic moment of a particle is

.

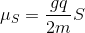Since S is an operator, this also means that the magnetic moment,

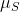, is an operator? This kind of confuses me. Is the "length" of

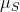given by the root of the eigenvalues of

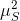, which would be

?

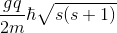Lastly, I'm guessing that to answer the question "How many beams does hydrogen produce from a Stern-Gerlach analyzer with a weak magnetic field?", you just count the number of different values you get for the total magnetic moment?

Thanks!

 

[Twigg]

Those magnetic moments don't look right on a first glance. They shouldn't be integer values of the bohr magneton. Did you calculate the correct g-factor for the hyperfine splitting?

yes, magnetic moment is an operator. It's proportional to spin. These numbers you are calculating are the eigenvalues. Since moment is proportional to angular momentum, the eigenstates of magnetic moment are the spin eigenstates (a diagonal matrix times a constant is still diagonal). And yes, your formula for the magnitude of the dipole moment looks correct if you're only considering a free electron. In general, the magnetic moment will vary with the overarching angular momentum of the system (vector sum, like you mentioned). But then, the value of g changes accordingly. we rarely talk about the magnitude of the magnetic moment because 90% of the time we are interested in the coupling between magnetic moment and a B-field, given by $V = -\mu \cdot B$. Can't think of any cases where the magnitude of moment matters, but I'm sure that there is someone out there who can prove me wrong :)

Yeah, that sounds right as far as SG beams

 

[Twigg]

Also the number of the hyperfine splittings is definitely wrong.

Like you said, you have to do the vector sum of L,S, and I for the hydrogen ground state. What F states does that give you?

 

[Trettman]

Hmm, that's odd. Our professor thought that the problem was a bit too tricky and gave us some extra info: he said that the perturbation is the sum of the hyper fine and Zeeman energy, and that the perturbation matrix in the coupled basis is given by

$$ W =
\begin{matrix}
\mu_B B + A/4 & 0 & 0 & 0 \\
0 & A/4 & 0 & \mu_B B\\
0 & 0 & -\mu_B B + A/4 & 0 \\
0 & \mu_B B & 0 & -3A/4
\end{matrix}
$$

and that the energy corrections [; E^1 ;] are the eigenvalues of W. He also said that the magnetic moment for a weak magnetic field is given by [;\mu = \partial E^1/\partial B ;]as B → 0. This gave me [; \mu_1 = \mu_B, \mu_2 = -\mu_B, \mu_3 = \mu_4 = 0 ;].

 

[Twigg]

Ok I think I am on the same page now. Disregard what I said about the magnetic moments being non-integer. In reality, they will not be integers, but it seems that your course is trying to focus on the fundamentals without getting bogged down in those details (that's a good thing).

This gave me [; \mu_1 = \mu_B, \mu_2 = -\mu_B, \mu_3 = \mu_4 = 0 ;].

Those are the correct moments. What I was commenting on before was that there should be four moments, not two.

For the record, if you're still confused about how magnetic moments are calculated, this is not how it's usually done, but this is also a valid approach. There is a much easier way, which allows you to write down the B-field dependent part of the diagonalized perturbation matrix without much thought. The trick is whenever you couple two angular momenta together, whether it's L and S, or nuclear spin (I) and total electronic angular momentum (J), you get a new total momentum (in the case of spin-orbit coupling, it's $\vec{J} = \vec{L} + \vec{S}$, and in the case of hyperfine splitting, it's $\vec{F} = \vec{I} + \vec{J}$). As a general rule, the new angular momentum operator will have it's own associated magnetic moment associated with it's Zeeman sublevels. For hydrogen, you have J = 1/2 and I = 1/2 (proton has a spin of 1/2), so you have the possibilities of F = 0 or 1, meaning you get m_F states 0,-1,0, and 1. The magnetic moment of each of these is just the value of m_F times hbar (and a g-factor, as I mentioned above, which isn't so easy to calculate). No diagonalization required, at least as far as magnetic moments are concerned.

 

[Trettman]

Oh, sorry, I thought you meant that the values were wrong!

Okay, I think I'm beginning to understand, but I'm still confused as to how you'd calculate the total magnetic moment in this problem. Is it just m_F*hbar*g+mu_i? If this is the case, then the total amount of beams hydrogen would produce in a Stern-Gerlasch analyzer would be 4*3=12, right? (Four m_F states and three mu_i-values).

Also, what does F and I represent? I haven't seen them used in the course (for reference, we're using Griffith's Introduction to Quantum Mechanics).

Thank you for your replies so far! It's really appreciated :) I hope I don't seem as blockish as I feel

 

[Twigg]

No worries. This stuff is confusing at first, and I wish someone had sat down with me when I saw it the first time :)

Let me answer your question about interpreting I and F first. This should clear up a lot of things at once. I is the total spin quantum number of the nucleus. Suppose you have a big ol' nucleus with, I dunno, 40 total particles. Every proton and neutron in that nucleus has a spin of 1/2. Because of the interactions between these individual particles, the nucleus has a (very very strongly) preferred total spin number. That number is I. For example, in hydrogen I = 1/2, because there's only one proton. Proton's have a spin 1/2, so you know that for hydrogen, I=1/2. To give you some other examples, consider the two most common isotopes of rubidium: $^{85}Rb$ and $^{87}Rb$. They both have 37 protons, but $^{85}Rb$ has two fewer neutrons than $^{87}Rb$. There's no easy way to guess the value of I in general, but you could look it up and you'd see that for $^{85}Rb$ you have I = 5/2 and for $^{87}Rb$ you have I = 7/2. The important thing is that you know the total spin. Think of I the same way you'd think about S, except I refers to nuclear spin and S refers to electron spin.

F is like J in that it is a total angular momentum, but F is more complete because F includes I where J does not. More explicitly, F = I + L + S whereas J = L + S. F is the total angular momentum of the atom, which includes the electron orbit, the electron's spin, AND the nuclear spin. The spin of the nucleus, considered by itself, has its own magnetic moment $\mu_{I,m_{I}} = g_{I} \mu_{B} m_{I}$. But this isn't the complete story, because the electron has it's own magnetic moment, $\mu_{j,m_{j}} = g_{J} \mu_{B} m_{j}$. In the hydrogen ground state (1s), L = 0 so J = S, and thus you can talk about the electron's spin magnetic moment by itself, since there's no orbital magnetic moment. Thus, $\mu_{j,m_{j}} = \mu_{s,m_{s}} = g_{S} \mu_{B} m_{s}$. The hyperfine structure arises because the nuclear magnetic dipole moment interacts with the spin magnetic dipole moment, just like two bar magnets would. This interaction means that eigenstates of the electron spin operator ($|s,m_{s}\rangle$) and nuclear spin operator ($I,m_{I}\rangle$) are no longer eigenstates of the complete Hamiltonian including the hyperfine interaction. Formally, $H|I,m_{I}\rangle|s,m_{s}\rangle \neq E |I,m_{I}\rangle|s,m_{s}\rangle$. So, you need to find the eigenstates of the hyperfine interaction. To do this, you inspect your hyperfine Hamiltonian, and you'd see that it depends on $\vec{I} + \vec{J}$, aka $\vec{F}$. Since it only depends on F, the eigenstates of the Hamiltonian are simply the eigenstates of F.

As far as the magnetic moments, in the limit as B -> 0, the coupling between the nuclear and electronic moments dominates the Zeeman splittings, so the system is strongly coupled (i.e. you can still think of F as the total angular momentum), and the magnetic moments are given by $g_{F} \mu_{B} m_{F}$. When you continue to ramp up the B-field, this approximation breaks down. You can see that the perturbation matrix W isn't diagonal. The Zeeman shift and the Hyperfine interaction don't commute. For large enough B, the Zeeman splitting eventually dominates the hyperfine splitting, and in the limit of B -> infinity, the nuclear spin and electron spin are completely decoupled and you return to a magnetic moment of $\mu = g_{J} \mu_{B} m_{j}$, the same magnetic moment you had back when you ignored the nucleus.

In the context of your problem, you are interested in the weak-field (low B) limit.

 

[Trettman]

Okay! Thank you very much for the well-written reply! Like I said, I really appreciate you help :) I feel like I finally understand most of this, except how I'm supposed to answer the question, as I'm still a bit confused about exactly what that pertubation matrix represents: it says that it's the sum of the hyperfine and Zeeman energy, so my first thought was that in order to calculate the total magnetic moment (the answer to the question), you calculate the magnetic moment which arises from the electron's and proton's spin (which would be [; g_F \mu_B m_F;] ?) and then add the magnetic moments that were calculated from the pertubation matrix, [;W;]. Is this correct? Or are the magnetic moments that were calculated from the pertubation matrix the answer to the question, since it says that the matrix is written in the coupled basis?