Is the Total Radial Force on a Current-Carrying Hoop Zero?

[etotheipi]

I was just reading through these lecture notes regarding the stresses in solenoids, and came across the following regarding a current-carrying ring orthogonal to a uniform magnetic field,

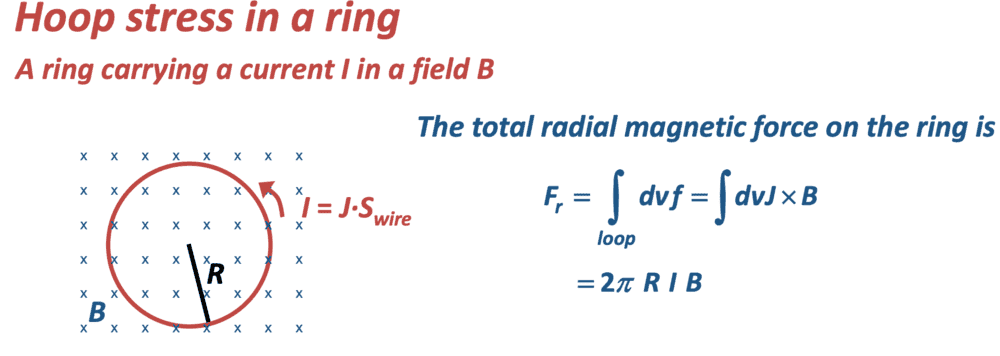
I wondered if this is a piece of terminology that I haven't come across? To me the total radial force is $\vec{0}$; they seem to be ignoring that the radial forces (vectors!) on each small piece of the ring cancel when the integral is taken around the whole loop! I hoped someone could clarify whether you'd agree that the above is incorrect. Thank you!

 

[BvU]

The vector sum is 0, so the ring isn't forced away from its current position.
The above is correct in the sense that the total radial force is not zero and causes the ring to be compressed -- which seems to be the topic at hand.
[edit] I say compressed, his next sheet says expanded -- what do you think ?

 

[etotheipi]

The vector sum is 0, so the ring isn't forced away from its current position.
The above is correct in the sense that the total radial force is not zero and causes the ring to be compressed -- which seems to be the topic at hand.

Thanks, I think that's probably what they mean. I still think the usage is a little odd... we might better say that the radial component of force on a small segment is non-zero.

Really what they've called $F_r$ seems to be the sum of the magnitudes,$$F_r = \int |d\vec{F}|$$and it doesn't seem like too useful a quantity, but hey ho!

 

[etotheipi]

[edit] I say compressed, his next sheet says expanded -- what do you think ?

I agree with you

 

[BvU]

doesn't seem like too useful a quantity

Helps calculate how much collar is needed -- often quite a lot !

 

[etotheipi]

That part is fine to me, because they're just showing the body forces acting on that piece on the left.

My issue was just with their notion of "total" radial force... it's a bit like exerting a force of 1N on each side of a 3D cube and claiming that the total radial force is 6N, when of course we would either say the net force has a magnitude of 0N or that the force on any given side has a magnitude of 1N.

Maybe the integral of magnitudes is useful for something like data tables, though

 

[BvU]

on each side of a 3D cube

What if it's a hollow paper cube ? Crumples !

 

[etotheipi]

What if it's a hollow paper cube ? Crumples !

Well yes, but IMO we could still analyse the situation perfectly well with standard quantities, namely the radial/tangential/normal stresses, which we might derive from components of forces acting on small sections of paper. There is no apparent need to define some weird new quantity which is just the magnitude of the radial force per unit area integrated up around the surface - even less so if the surface is not nice and uniform like a sphere!

 

[pbuk]

There is no apparent need to define some weird new quantity

This is not any weird new quantity, the author is simply referring to the sum of the magnitude of the force (which is of course very useful for calculation of stresses) and this is clear from the term 'total radial force'.

If the author had wanted to refer to the vector sum of the forces then he would have written that, or alternatively the 'net [radial] force'.

Conventionally, total ≡ aggregate ≡ sum of magnitudes; net ≡ vector sum.

 

[etotheipi]

Fair enough, though I have never seen that distinction made before. To me "total" and "net" are synonyms because forces are inherently vector quantities, and all physical laws are formulated as such (e.g. we write $\sum \vec{F}_i = \dots$, etc). Perhaps this is a mechanical engineering convention?

In any case it's clear to me now what the author intended (whether or not it's a good idea is another question ), so thank you!

 

[BvU]

It's good to be critical, but I think you are a bit too rigid. Carmine introduces the subject in a sensible way.
It reminded me of the huge 'force' (pressure * area) needed to squeeze an eggshell .

To his credit (don't you think?) he rapidly changes over to pressure (not a vector ) / stress (a tensor !)

 

[etotheipi]

It's good to be critical, but I think you are a bit too rigid. Carmine introduces the subject in a sensible way.
It reminded me of the huge 'force' (pressure * area) needed to squeeze an eggshell .

To his credit (don't you think?) he rapidly changes over to pressure (not a vector ) / stress (a tensor !)

Perhaps, but what he did essentially amounted to multiplying by $2\pi$ and then multiplying by $\frac{d\theta}{2\pi}$, which seems unnecessary. I would just write it like this; consider a small element in static equilibrium,$$dF_r - 2T\sin{\frac{d\theta}{2}} \approx BIR d\theta - Td \theta = 0 \implies T = BIR$$no need for any "total radial force"!

To be honest, you're probably right that I'm being pedantic; I was reading through it quite late and I get slightly irritated whenever `I come across these unnecessary complications, especially when I'm tired .

But as your eggshell example demonstrates, maybe there is a place for the term. Though I suspect it's more useful as a comparative measure, and not for calculations.

 

[pbuk]

Fair enough, though I have never seen that distinction made before. To me "total" and "net" are synonyms

"Total" and "Net" are not synonyms; in many usages they are antonyms (If I walk 500 metres to the shop and back what is the total distance I have travelled? And the net distance?). I can't think of an example in science, engineering or elsewhere that we use the word 'net' except where it is useful in order to distinguish it from 'total'.

To me "total" and "net" are synonyms because forces are inherently vector quantities

What is the total pressure (force) on a submerged object? And what is the net pressure force?

 

[pbuk]

maybe there is a place for the term. Though I suspect it's more useful as a comparative measure, and not for calculations.

What is the total pressure (force) on a submerged object? And what is the net pressure force?

Please don't design any submarines until you have resolved this misunderstanding

 

[etotheipi]

If I walk 500 metres to the shop and back what is the total distance I have travelled? And the net distance?

Distance is an integral of speed, so of course it is strictly positive. Net distance doesn't make sense.

I can't think of an example in science, engineering or elsewhere that we use the word 'net' except where it is useful in order to distinguish it from 'total'.

Both 'net' and 'total' to me imply a summation, and that they are interchangeable. Note also that the Wikipedia page for 'Net Force' uses the heading 'total force' for the section on vector addition. In most other mechanics notes I have studied, net and total are also used interchangeably. All of the following, to name a few, use the phrasing 'total force' or 'total external force' to refer to the the vector sum:

https://www.damtp.cam.ac.uk/user/tong/dynamics/clas.pdf
https://www.dpmms.cam.ac.uk/~stcs/courses/dynamics/lecturenotes/section5.pdf
http://www.southampton.ac.uk/~stefano/courses/PHYS2006/chapter1.pdf

Respectfully, I would be interested to see where you obtain this distinction in terminology from.

What is the total pressure (force) on a submerged object? And what is the net pressure force?

I would say that the total/net pressure force on a submerged object is $$\vec{F} = \int_S p \, d\vec{A}$$which, if the density is constant, can be shown to resolve to Archimedes' principle.

If you were to analyse the stresses in the material of a spherical shell (of a submarine, for examples sake), I would consider a small element of the surface. Presumably we would also have a spatial variation of surface forces, too, so simply summing the magnitudes would not be so helpful.

 

[pbuk]

Distance is an integral of speed, so of course it is strictly positive. Net distance doesn't make sense.
...
Respectfully, I would be interested to see where you obtain this distinction in terminology from.

Restricting myself just to net distance, here are three examples from papers on Biology, Quantum Field Theory and Computer Science:

• https://www.damtp.cam.ac.uk/user/lauga/papers/32.pdf "The net distance traveled by the swimmer does not depend on the rate at which it is being deformed, but only on the geometrical sequence of shape "
• https://www.damtp.cam.ac.uk/user/dbs26/AQFT/chap3.pdf "... a very famous property of random walks: that after a time interval $t$, one has moved through a net distance proportional to $\sqrt t$ rather than $t$ itself."
• https://core.ac.uk/download/pdf/82374355.pdf "Finally, we consider the trivial Net Distance: [equation]. Its main use is in the definition of the (possibly fractal) dimensional width W of a connected finite net..."

I would say that the total/net pressure force on a submerged object is $$\vec{F} = \int_S p \, d\vec{A}$$which, if the density is constant, can be shown to resolve to Archimedes' principle...

I would say that the net pressure force is the buoyant force and is proportional to volume and (assuming an incompressible fluid) constant with depth. The total pressure force is proportional to surface area and also proportional to depth.

 

[etotheipi]

These are all quite different usages of the term, though, and it's quite apparent what's being implied by context. For instance, for the random walk, when he writes

after a time interval $t$, one has moved through a net distance proportional to $\sqrt{t}$ rather than $t$ itself

he is really just referring to the magnitude of the displacement (the distance between the start and end points) as opposed to the total distance along the zig-zag.

I would say that the net pressure force is the buoyant force and is proportional to volume and (assuming an incompressible fluid) constant with depth. The total pressure force is proportional to surface area and also proportional to depth.

So long as we know what we're talking about maybe your naming convention is understandable, but I think it is slightly misleading.

The "total pressure force" you define is not a force, it is a sum of magnitudes of forces around the surface. If anything, I would call it explicitly the "total of the magnitudes of the pressure forces".

For me, the total pressure force is that which acts through the centre of pressure:

The center of pressure is the point where the total sum of a pressure field acts on a body, causing a force to act through that point. The total force vector acting at the center of pressure is the value of the integrated vectorial pressure field.

https://en.wikipedia.org/wiki/Center_of_pressure_(fluid_mechanics)

 

[pbuk]

For instance, for the random walk, when he writes "after a time interval , one has moved through a net distance proportional to rather than itself" he is really just referring to the magnitude of the displacement (the distance between the start and end points) as opposed to the total distance along the zig-zag.

So are you saying that there is a distinction between "total distance" and "net distance" and that the terms can be used unambiguously without further qualification? This seems to be exactly the opposite of what you have been arguing.

 

[etotheipi]

So are you saying that there is a distinction between "total distance" and "net distance" and that the terms can be used unambiguously without further qualification? This seems to be exactly the opposite of what you have been arguing.

`I might have well said the "total distance between the start and end points". The point is that it's a completely different context. I'd never heard the term 'net distance' before but as far as I can tell, in these examples, it's just a translation of 'magnitude of displacement'. In any case, I think it's a bad terminology also.

Force is a vector, and total force is also a vector. The "total force" you defined is not a vector, it is the surface integral of pressure times the scalar area.

The usage of total force being synonymous for net force is abundant in the literature, and I would very skeptical of anything said to the contrary.

 

[pbuk]

`I might have well said the "total distance between the start and end points". The point is that it's a completely different context. I'd never heard the term 'net distance' before but as far as I can tell, in these examples, it's just a translation of 'magnitude of displacement'. In any case, I think it's a bad terminology also.

If the rules of this game are "every example you can find I will decide is a special case that does not disprove my general hypothesis, and is wrong anyway" then I don't think there is much point in playing. It is an interesting way to approach science.

The usage of total force being synonymous for net force is abundant in the literature, and I would very skeptical of anything said to the contrary.

I prefer the terms 'resultant force' or 'sum of forces' as it removes any ambiguity. Let's see: https://www.dpmms.cam.ac.uk/~stcs/courses/mechanics/lecturenotes/L2_L3.pdf 9 hits for 'resultant', 9 for 'sum of' and 2 for 'total' (both 'total moment').
https://www.brown.edu/Departments/Engineering/Courses/En4/Notes/Forces.pdf 8 matches for 'resultant', 1 for 'total' and 1 for 'sum of'.

Force is a vector, and total force is also a vector. The "total force" you defined is not a vector, it is the surface integral of pressure times the scalar area.

http://www.damtp.cam.ac.uk/user/mem/FLUIDS-IB/dyn.pdf "Pressure forces are strictly speaking isotropic, i.e. direction-independent, by definition. This means that they are described by a scalar fieldp(x,t) (called the pressure)..."

 

[etotheipi]

http://www.damtp.cam.ac.uk/user/mem/FLUIDS-IB/dyn.pdf "Pressure forces are strictly speaking isotropic, i.e. direction-independent, by definition. This means that they are described by a scalar fieldp(x,t) (called the pressure)..."

I don't know what your point is here. Pressures are isotropic. When you multiply the pressure by a directed unit vector, you obtain the force.

Strictly speaking, hydrostatic pressure is described by the stress tensor in the form $\sigma_{ij} = -p\delta_{ij}$ and the pressure is one third the trace. The $i$th component of force due to the pressure is$$dF_i = \sigma_{ij} d{S}_j$$and you can integrate that over a surface to obtain the total/net force in the $i$th direction.

As for your example, the scalar field $p(\vec{x}, t)$ is not a force field, it is a pressure field.

I prefer the terms 'resultant force' or 'sum of forces' as it removes any ambiguity. Let's see:

I like all of those terms, but 'resultant force', 'sum of forces', 'total force', 'net force', all mean the same thing.

 

[fresh_42]

Temporarily closed for moderation.

 

[fresh_42]

I like all of those terms, but 'resultant force', 'sum of forces', 'total force', 'net force', all mean the same thing.

I don't think this can be said this way. We wouldn't use different words if that was the case.

• resultant force: vector addition
• sum of forces: ambiguous, since it is not clear whether forces are considered as vectors or as magnitudes here, or even as a collection of forces (all forces which apply to a certain object: pull, drag, friction, buoyancy etc.)
• total force: sum of all magnitudes (in the context of this thread)
• net force: resulting force after vector addition

Not only is language highly context sensitive, words in a scientific text can be, too. It only makes sense to speak of a net force if there is another term, too. @pbuk explained his point of view in post #13 and the discussion could have ended there. The picture with a walk around a lake to distinguish total distance and net distance was clear. And distance has the same problem as forces have: considered as vector or as scalar? As I see it only velocity and speed give us the luxury to distinguish vector and scalar. Net something is commonly used as a result, and total something already starts to be context sensitive. If used beside net, then it is the absolute values.

I re-open this thread, but please end this argumentation about vectors if they have not been formally defined.

 

[etotheipi]

As I feared, I am still not convinced. I can perhaps agree that the terminology is context dependent.

I do not mean to invoke "proof by reference to eminent authority", but I feel obliged to mention that every reference I have consulted (the Feynman lectures, dynamics notes from https://www.dpmms.cam.ac.uk/~stcs/courses/dynamics/lecturenotes/section5.pdf, https://courses.maths.ox.ac.uk/node/view_material/1893, MIT, Caltech, and many others) use total force to refer to the vector sum of forces, or force components. l believe everything I have said is very much mainstream terminology .

In any case, I shall not pursue this further. Thanks everyone for helping.

 

[phinds]

In any case, I shall not pursue this further.

You just did.

 

[pbuk]

If you do come back to this you might like to look at page 118 (in print, p124 of the PDF) of the first set of notes you referenced (https://www.damtp.cam.ac.uk/user/tong/dynamics/clas.pdf).

"As the particle makes its little Larmor circles, it feels a slightly stronger force when it’s, say, at the top of its orbit where the field is slightly larger, compared to when its at the bottom. This net force tends to push the particle to regions of weaker or stronger magnetic field."

I can only find the word 'total' once in relation to force in these notes: "...where we’ve defined the total external force to be $\textbf F^{ext} = \Sigma_i \textbf F^{ext}_i$". This is a good way to go: where a term is potentially ambiguous, define it. Presumably the author felt that the term "net force" is sufficiently unambiguous not to require a definition.

That looks like a great set of course notes BTW, and a good list of recommended reading at the front. Of the three classic texts, I prefer the more rigorous treatment in Arnold.

 

[etotheipi]

You just did.

Hold on to your hats, because I'm about to do it again...!

On a serious note, apart from the notes I linked in the very first post, I have yet to find a single reference that defines 'total force' in the way @pbuk and @fresh_42 have defined here.

I would be very grateful if someone could direct me to a reference on classical mechanics (or, at this point, anything) where this distinction is explicitly made.

Thanks

 

[pbuk]

I would be very grateful if someone could direct me to a reference on classical mechanics (or, at this point, anything) where this distinction is explicitly made.

It is going to be hard to find anything in dynamics because as you have pointed out in this topic we are only ever interested in the vector sum of forces (resultant force).

Searching some relevant topics in statics/engineering/materials science would be more fruitful. Here's a few suggestions, I'll leave it to you to follow these up.

• https://www.google.com/search?q=statics+"total+force"
• https://www.google.com/search?q=pressure+vessel+"total+force"
• https://www.google.com/search?q=stressed+member+"total+force"

If you want to restrict yourself to a certain institution add +site:ic.ac.uk (or +site:cam.ac.uk, +site:mit.edu etc.) to the end of the query string.

Edit: forum couldn't auto parse quoted strings in URLs, fixed with s/"/%22

 

[etotheipi]

Thanks, but I followed the links individually and couldn't find anything.

The first hit under https://www.google.com/search?q=statics+"total+force" was:

where total force is the vector sum, integrated over the element.

The first hit under https://www.google.com/search?q=pressure+vessel+"total+force" was

and again, the total force here is the pressure times the projected area, which equals the vertical component of the resultant force (not the sum of the magnitudes, which would be what we obtain if we integrated the magnitudes over the real area).

These all appear to support my position...

My issue is this. As a student, I can only judge what is "true" by the evidence presented to me. On the one hand, I have come across a multitude of resources (the above included) that define total force in the way I suggested.

On the other hand, experts like yourself and @fresh_42 have suggested it is defined differently. But I cannot accept this definition for two very big reasons. Firstly, I have come across no references for it. I think the burden of proof is on the party suggesting the new definition. Second of all, I see very limited circumstances in which your definition can be used, and in the vast majority of the literature the meaning is the one I have presented.

With that considered, I will continue to employ my current usage of the term. I will also, respectfully, reject your definition unless it is supported by a reference.

 

[hutchphd]

With respect, I believe this reference from a 19 century mathematician should conclude the discussion.