vs55
- 20
- 0
Homework Statement
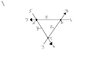
the following statement shows the traffic flow(in cars/minute) along 3 one way streets through the intersections A, B and C
Set up and solve a system of linear equations(using the augmented matrix for the system) to help you find the flows x,y and z. Be sure to generate the RREF of the system
a link of the drawing:
http://img18.imageshack.us/img18/2276/trafficflow.jpg
Homework Equations
traffic flow in must equal flow out
The Attempt at a Solution
so to start things off, equations i put:
3 + z = 3
6 + x = 7
5 + y = 4
is this at all right?
Attachments
Last edited by a moderator: